Can a policy with gaussian distribution allow two distinct optimal actions to have distinctively high probabilities?

Question

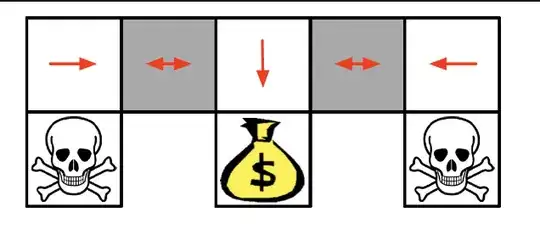
As an example to show the benefits of stochastic policy, I often have seen the below grid world example. Five blocks in a row. the first, third, and fifth are white(distinguishable states), and the second and fourth are gray(for agent, these two states are equivalent, non-distinguishable). positive reward if goes down in the middle state, negative reward if goes down in the first and the fifth states. They often say, in the gray region, it's best to put 0.5 probability to each left and right actions and it is possible only by stochastic policies.

Let Left = 0, Down = 1, and Right = 2 be action values. Let those three actions, left, down, right be available for all states, that down action in gray state will just let it stay with negative reward. My question is, for the gray region, if we use gaussian distribution for our policy, can we set up 0.5 probability for each left and right action? wouldn't it naturally make the probability to choose down action quite high as we only modify mean and variance value?

I just thought it's interesting that most RL paper seems to use gaussian distribution for stochastic policy but that distribution cannot even solve this simple setup, which is often used in teaching the benefits of stochastic policy. Or, am I wrong?

Answer 1

Assuming by distinct you mean that, for example, the euclidean distance between the two actions is sufficiently large, then no it cannot be true. This is because the Normal distribution is uni-modal. There is an interesting paper that uses this fact as motivation to replace Normally distributed action selection in on-policy optimisation of MuJoCo tasks with discretised variants since a discrete (e.g. softmax) distribution can be multi-modal.

An alternate to discrete actions could be to use a mixture of Gaussians. This allows the modelling of multiple-modes, and in particular if you have prior information about your action space that informs you how many modes there are likely to be, it goes a long way to knowing how many Gaussians in the mixture you'd need. An example of this being used, whilst not directly to parameterise the action distribution, is in Distributional RL, where the returns are modelled as a probability distribution. The authors of this paper look to use MoG as an alternative to the commonly used C51 parameterisation (modelling the returns with a discrete distribution of 51 evenly spaced atoms) since this typically requires knowing the lower/upper bounds of your returns, whereas MoG is defined over the whole real line so doesn't require this prior information.

For what it's worth, a Normally distributed policy would not be applicable to the example you have given, since this looks to be an environment with a discrete action space.