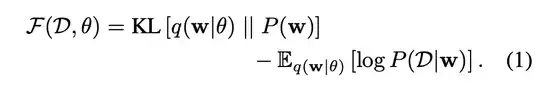KL loss not changing in a Bayesian Neural Network?

Question

I've been trying to train a Bayesian Neural Network and I noticed that the KL loss (which enforces the prior) isn't changing over time. And it occurred to me that while in standard Bayesian inference the prior acts like an artificial dataset (e.g. beta(N,N) adds 2N more observations). In Bayesian Neural networks like Bayese-by-Backprop, the prior is just a regularizing term in the loss function (the KL loss term).

Which as I understand it means the KL loss term might never increase (depending on its weight), and thus uncertainty might never decrease, which contradicts the standard Bayesian inference behavior where the prior is guaranteed to lose it's importance as you get more data... Further more if you play with loss term weights then there is a question as to what weights are valid & how to prevent collapse to a fully deterministic network...

Please tell me I'm wrong, and explain how (hopefully) this is fully comparable to regular Bayesian inference as well as why KL-loss might not change during training?

Answer 1

This looks like more underfitting than other issue.

But you are overlooking that Bayes by Backprop is an approximation to Bayesian principles, because a true Bayesian NN is not tractable, you are using an approximation, and it behaves approximately, so not all principles you mentioned actually apply.

Answer 2

Your observation is correct. In BNNs trained with methods like Bayesian by backprop (BBB), the KL loss serves as a regularizer that encourages the posterior distribution of weights to approximate the prior distribution, therefore it's possible for the KL loss to remain relatively constant during training, especially if the model has not yet learned to deviate significantly from the prior meaning it's actually learning well w.r.t the prior as expected or the weights are initialized close to the prior. In BNNs and ML in general the prior remains fixed throughout training to be qualified as a regularizer for reducing test error, while in standard Bayesian inference the prior is continuously updated based on newly observed data without generalizable learning or prediction consideration. Though bearing in mind such functional difference, in principle BNNs are designed with the same aim as Bayesian inference to decrease prior uncertainty with more training data.

BNNs training sometimes can readily lead to undesirable underfitting behavior, such as "posterior collapse" to a deterministic network caused by the complex interactions between the architecture of the neural network, the choice of prior, the amount of training data and the KL loss weight. For instance, your prior is put too much weight due to your confidence but the data is actually in total conflict with your prior, which is possible to fit your specific case. The loss of uncertainty propagation and update of learnable parameters defeats the purpose of employing Bayesian method which is crucial for robust decision-making.

Balancing KL loss weight hyperparameter is often an empirical process and it depends on factors like the model capacity and the amount of available data. The more effective capacity or lesser training data, the larger the hyperparameter in general. Also techniques such as the use of a fixed schedule for annealing the KL weight could mitigate the "posterior collapse".