In "Artificial Intelligence: A Modern Approach", the authors say that the space complexity of depth-first search is proportional to O(bm), considering b as the branching factor and m the maximum depth of the graph. But it is not obvious why, for me.
The algorithm for searching graphs involves storing the explored nodes in the explored set, and the nodes open, but not explored yet, are stored in the border set.
Let us consider the following graph, with the start node in green and the end node (the goal) in red.
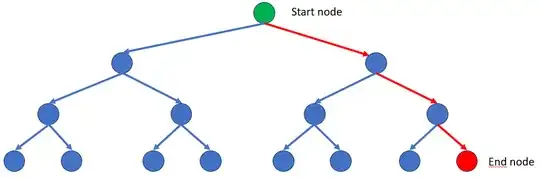
The solution is given by the red path.
But, in my perspective, in this scenario, in the worst case, the algorithm would try every path from the root to each leaf, and store all the nodes in the explored set.
Thus, if we consider this, the space complexity is, at least, proportional to $O(b^m)$.
Is there something wrong with this reasoning?
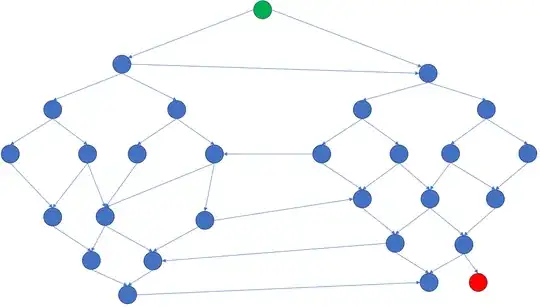
I'm including another image to represent better the searching process on a graph.
Best regards.