I would like to know why the vanishing gradient problem especially relevant for a RNN and not a MLP (multi-layer-pereptron). In a MLP you also backpropagate errors and multiple different weigths. If the weights are small, the resulting update in the last layers in the backpropagation will be very small
-
In the most simple case, you can think of RNN as a recursive MLP that calls itself multiple times. We can unfold it into a very deep MLP and as a result, the gradients vanish as they propagate through the numerous layers. – Aray Karjauv Jan 09 '24 at 16:57
3 Answers
No, ResNet were not introduced to solve vanishing gradients, citing from the paper:
An obstacle to answering this question was the notorious problem of vanishing/exploding gradients [1, 9], which hamper convergence from the beginning. This problem, however, has been largely addressed by normalized initialization [23, 9, 37, 13] and intermediate normalization layers [16], which enable networks with tens of layers to start converging for stochastic gradient descent (SGD) with backpropagation [22].
However, vanishing gradient happens also for MLP for the same reasons why they happen in RNNs as you can see an unrolled RNN as a MLP at the end of the day: because you stack multiple layer, and if many of them saturate, the gradient will tend to zero
You can see it from an unrolled RNN:
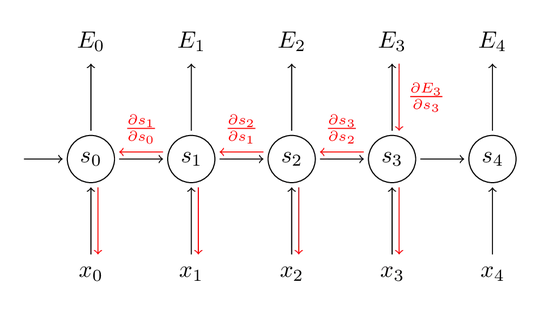
Here, the gradient of $E_4$ with respect to $x_0$ will have to travel 6 matrix multiplications/non linearities, even though the net is just 1 layer deep.
If the spectral norm of such matrices is less than one (ie the highest eigenvalue is < 1), then they are contractive, and thus a vector multiplied many times by such matrix will be attracted to 0
- 2,863
- 5
- 12
Vanishing gradient problem is indeed present in MLP and CNNs. Please have a look at ResNet paper: before the introduction of residual blocks, the vanishing gradient problem was one of the main limitations to the depth of the networks. In RNNs this problem is present also with fewer layers because each layer needs to perform backpropagation through time, so learning is additionally constrained by the sequence length.
- 410
- 3
- 9
Two problems for RNNs
- They're typically "deeper" than a MLP since you can unroll a RNN into a stack of layers for each timestep, which exacerbates the problem
- The activation function of choice typically is tanh which has diminishing gradients at the extremes
- 21
- 1