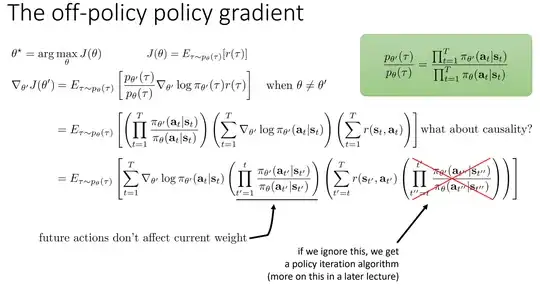
While this may be apparent to many, I'll provide an answer anyway.
In a nutshell, 2 steps:
- Bring the distribution from $\theta$ to $\theta '$ to cancel the importance ratio term. Use causality to simplify the cumulative reward term to reward-to-go. Details can be found here, which utilized Expected Grad-Log-Prob Lemma.
- Bring the distribution back to $\theta$. Use distribution law and the definition of marginal distribution to get the final formula.
proof:
\begin{align}
&\mathop{\mathbb{E}}_{\tau\sim \theta}\left[ \left( \prod_{t=1}^{T} \frac{\pi_{\theta '}(a_t|s_t)}{\pi_{\theta }(a_t|s_t)} \right)\left(\sum_{t=1}^{T}\nabla_{\theta'}\log \pi_{\theta '}(a_t|s_t) \right) \sum_{t=1}^{T}r(s_t,a_t)\right] \\
=&\mathop{\mathbb{E}}_{\tau\sim \theta '}\left[\left(\sum_{t=1}^{T}\nabla_{\theta'}\log \pi_{\theta '}(a_t|s_t)\right) \sum_{t=1}^{T}r(s_t,a_t)\right] \\
=& \mathop{\mathbb{E}}_{\tau\sim \theta '}\left[\sum_{t=1}^{T}\left(\nabla_{\theta'}\log \pi_{\theta '}(a_t|s_t) \sum_{t'=t}^{T}r(s_{t'},a_{t'})\right)\right] \tag{causility} \\
=& \sum_{t=1}^{T} \sum_{t'=t}^{T} \mathop{\mathbb{E}}_{\tau\sim \theta '} \left[\nabla_{\theta'}\log \pi_{\theta '}(a_t|s_t)r(s_{t'},a_{t'}) \right] \tag{distribution law}\\
=& \sum_{t=1}^{T} \sum_{t'=t}^{T} \mathop{\mathbb{E}}_{\tau\sim \theta} \left[\prod_{{t''}=1}^{T} \frac{\pi_{\theta '}(a_{t''}|s_{t''})}{\pi_{\theta }(a_{t''}|s_{t''})} \nabla_{\theta'}\log \pi_{\theta '}(a_t|s_t)r(s_{t'},a_{t'}) \right]\\
=& \sum_{t=1}^{T} \sum_{t'=t}^{T} \mathop{\mathbb{E}}_{\tau\sim \theta} \left[\prod_{{t''}=1}^{t'} \frac{\pi_{\theta '}(a_{t''}|s_{t''})}{\pi_{\theta }(a_{t''}|s_{t''})} \nabla_{\theta'}\log \pi_{\theta '}(a_t|s_t)r(s_{t'},a_{t'}) \right] \tag{marginal distribution}\\
=& \mathop{\mathbb{E}}_{\tau\sim \theta} \left[\sum_{t=1}^{T} \nabla_{\theta'}\log \pi_{\theta '}(a_t|s_t)\sum_{t'=t}^{T} \prod_{{t''}=1}^{t'} \frac{\pi_{\theta '}(a_{t''}|s_{t''})}{\pi_{\theta }(a_{t''}|s_{t''})} r(s_{t'},a_{t'}) \right]\\
=& \mathop{\mathbb{E}}_{\tau\sim \theta} \left[\sum_{t=1}^{T} \nabla_{\theta'}\log \pi_{\theta '}(a_t|s_t)\prod_{{t''}=1}^{t} \frac{\pi_{\theta '}(a_{t''}|s_{t''})}{\pi_{\theta }(a_{t''}|s_{t''})}\sum_{t'=t}^{T} r(s_{t'},a_{t'})\prod_{{t''}=t}^{t'} \frac{\pi_{\theta '}(a_{t''}|s_{t''})}{\pi_{\theta }(a_{t''}|s_{t''})} \right] \\
\end{align}