Masking in Decoder of Transformer

Question

I understand that the masked multi-head attention block ensures that generation of token at time step t doesn't rely on subsequent tokens of the input. But the residual connection which adds the input to the output of masked multi-head attention block adds some of the information from future time steps which is then used to construct the query matrix for multi-head attention block.

Shouldn't some kind of mask be applied before adding the input values to the output of masked multi-head attention block as well?

Asking this question in the context of training process.

Answer 1

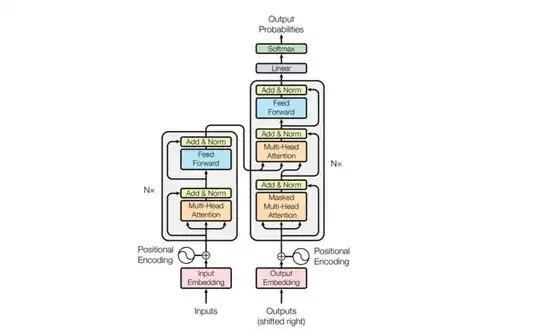
No, adding an additional mask to the residual connections or the linear layer isn't necessary. The masking is crucial solely for the attention mechanism. Implementing a mask in the residual connections or the linear layer would only reduce dimensionality and overly constrain the model's outputs. Remember, for the final output, it's essential that the model has full contextual information. Zeroing a value at any step would make the model less efficient by causing it to lose information.

It's important to note that even within the attention mechanism, the input data is already being utilized in the attention computation. This is evident after the masking of the attention weights, where the matrix $QK^T$ is projected again with the $V$ matrix, which is equal to $W_VX$. Where $X$ is the input data. Thus, worrying about retaining the mask output is unnecessary. Additionally, when multiplying with the $V$ matrix, you're already losing the lower triangular matrix. From that point on, adding the initial input doesn't pose an issue.

Another crucial aspect to consider is the significance of the residual layers. Without them, the positional information from the Positional Encoding (PE) would rapidly diminish, making it vital to retain these layers. So, even if, for some reason, it affects the property of not seeing future tokens (which it doesn't), you would still want to maintain the residual connections.