2

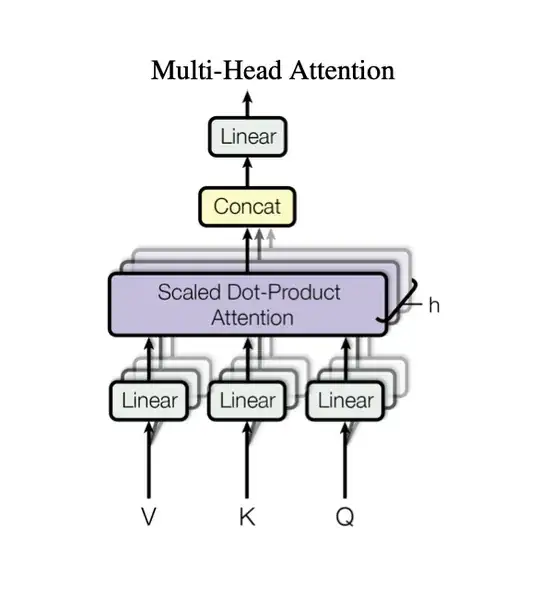
I have been trying to implement a Transformer architecture using PyTorch by following the Attention Is All You Need paper as well as the The Annotated Transformer blog post to compare my code with theirs. And I noticed that in their implementation of the Multi-Head Attention they have used three nn.Linear(d_model, d_model) to project the input of the encoder before splitting these projections into (n_heads, d_k) matrices for the attention. But as my understanding of the paper goes, we need to have n_heads of nn.Linear(d_model, d_k) for each of the queries, keys and values as we can see in the Multi-Head Attention's diagram here from the paper:

enter image description here

We clearly see as many nn.Linear layers as there are of heads. As well as the explanation of the authors:

enter image description here

Each $head_{i}$ uses $W_{i}^{Q}$, $W_{i}^{K}$ and $W_{i}^{V}$. So in my implementation I did this:

class MultiHeadedAttention(nn.Module):
  def __init__(self, d_model=512, h=8):
    super(MultiHeadedAttention, self).__init__()
    self.d_model = d_model
    self.h = h
    self.d_k = d_model // h
    self.query_linears = nn.ModuleList([nn.Linear(d_model, self.d_k) for i in range(h)])
    self.key_linears = nn.ModuleList([nn.Linear(d_model, self.d_k) for i in range(h)])
    self.value_linears = nn.ModuleList([nn.Linear(d_model, self.d_k) for i in range(h)])
    self.projection_layer = nn.Linear(h * self.d_k, d_model)

def forward(self, Q, K, V, mask=None):
    batch_size = Q.size(0)
    queries = torch.cat([linear(Q).view(batch_size, 1, -1, self.d_k) for linear in self.query_linears], dim=1)
    keys = torch.cat([linear(K).view(batch_size, 1, -1, self.d_k) for linear in self.key_linears], dim=1)
    values = torch.cat([linear(V).view(batch_size, 1, -1, self.d_k) for linear in self.value_linears], dim=1)


x = scaled_dot_product_attention(queries, keys, values, mask)

x = x.transpose(1, 2)
x = x.contiguous()
x = x.view(batch_size, -1, self.h * self.d_k)
x = self.projection_layer(x)
return x

But I'm surely missing a key piece of understanding. And I'd be really grateful if someone can point it out to me.

Thank you.

Daviiid
  • 585
  • 5
  • 17

1 Answers1

4

It is just an optimization technique.

If you have a vector $x$ of size $d$ and you want to multiply with $n$ different matrices $W_i$ of shape $d \times d_k$, then you could simply stack these matrices along the last dimension and perform a single matrix multiplication.

A block view of this matrix operation would look like this:

\begin{equation} x \underbrace{ \begin{bmatrix} W_0 & W_1 & \cdots & W_{n-1} \end{bmatrix} }_{\text{stack along the last dim}} = \begin{bmatrix} xW_0 & xW_1 & \cdots & xW_{n-1} \end{bmatrix} \end{equation}

Now instead of looping over all the matrices, you actually perform the forward pass with a single vector-matrix multiplication $xW$, where $W$ has shape $d \times nd_k$.

Another thing that the authors of the paper this is that they chose $n$ and $d_k$ such that $d = nd_k$. So if $d=512$ and you want to have 8 heads in the multi-head attention layer, then you set $d_k=64$. This was done so that no matter how many heads you chose to have, you always have the same number of parameters in the model. I guess it is easier to do hyperparameter search this way, but you don't have to do it if you don't want to.

If you want to see a more detailed blog post about the implementation details of the transformer model feel free to check out this: https://pi-tau.github.io/posts/transformer/

pi-tau
  • 995
  • 6
  • 12