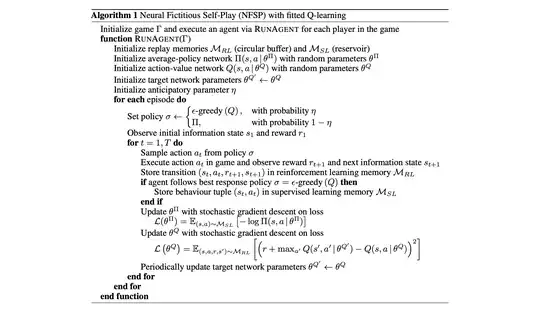
I was reading the NFSP player from D. Silver, and I'm somewhat confused by the algorithm:
In particular, given that we sample an action according to best response ($\sigma = \epsilon-\text{greedy}(Q)$), we also insert this transition in $\mathcal{M}_{RL}$, over which then we will estimate the gradient for the policy $\pi$... however, since this action has not been sampled from the policy $\pi$, it biases the gradient, which usually should be corrected by the importance sampling ratio
what am I missing?