Why clamp std for reparameterization trick between -20 and 2?

Question

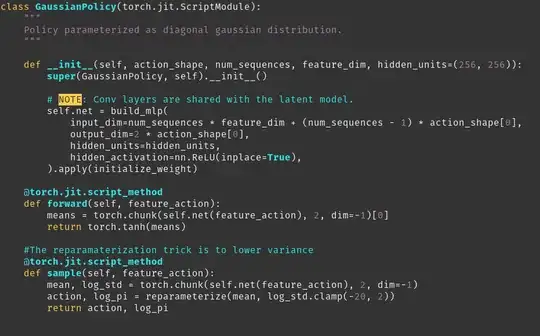
In the Soft Actor Critic Paper (found here https://arxiv.org/pdf/1801.01290.pdf), they use a neural network to approximate a diagonal gaussian distribution. In the sample function you can see that it has a function called reparameterize. As you can see in the reparameterize function, we use a tanh function to squash the action bound between -1 and 1. So why is it that we clamp the standard deviation between -20 and 2. I have read both Soft Actor Critic papers and can't find why we do this. Is there something about the normal distribution that would make that range of clamping of the std more desirable? Does bounding the range of the std help with convergence. Is there a paper you my recommend that would help with this answer? This is my first post here so if you need more information please let me know.

Link to code Repo

Answer 1

This is a common trick done in practice: this helps to stabilize training, and prevent large values that can blow up in NaNs.

The reason is that the std of the Gaussian is learned in log-space (because it's easier to learn with neural-nets) that is unbounded ($-\infty, +\infty$), and so you want to bound to something like $[-20, 2]$ because such log-std will be exponentiated later: you have $\exp(-20)\approx 0$, and $\exp(2) = 7.389$ that is reasonably small; a similar trick is also employed for log-probabilities.

Practical tricks like this one are often not documented in the paper (unfortunately), but can be found in code implementations.