1

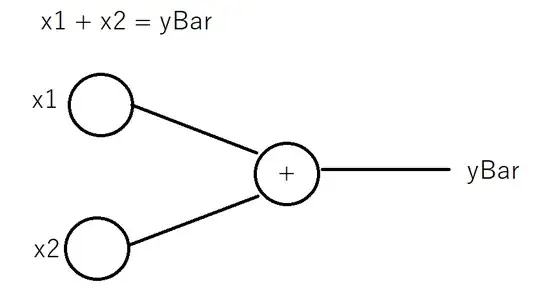
This might be unnecessary but to learn the basics of neural networks, I am trying to create a single perceptron neural network to solve the adding operation of 2 inputs (x1 + x2 = ybar)

The code is written in C# since the math should be very simple and it's a language I use usually more than python.

The problem is the network is not capable of learning the right weights for this simple problem so I am trying to understand why is that before checking another working example on the internet

Note before explaining more about the problem, feel free to include any level of math or technical stuff (although might not be needed for this simple question).

enter image description here

Learns is the time the backpropagation happens. So equal to the nb of batches. Activation function takes x and rounds it to the nearest integer. The cost function is yBar - y. The total cost for each batch is the sum of all the costs generated by the samples in that batch divided by the batch size (so the average). Backpropagation is in the form of w[i+1] = w[i] - learningRate * cost. The hope is that w1 and w2 should end up having the same value after backpropagation.

To test the code I tried first on 1 input:

enter image description here

It learns a combination of weights for that case to work.

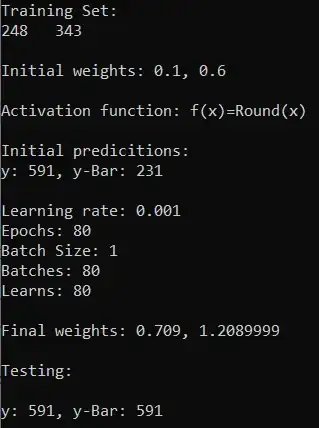
But then I tried generating a random training set of 500 rows and changing the batch size to 10 expecting it to generalize the problem and the weights to be in the form of w1 ~= w2. But it is failing to do so. Most of the predictions are away from the correct value by 30 or 40 with some exceptions that are far by a 100.

I am not sure about how to think of the problem. This is supposed to be a linear problem so the activation function should not be the issue. I suspected the way the cost is calculated might be the issue, but there doesn't seem to be a more fitting cost function for this adding operation. Tried changing the learning rate and the initial weights with being pretty sure that these are not the problem, and it also didn't work.

How to think of this problem ? What are the clues to look for in order to find the wrong parameter ? And how to fix it ?

EEAH
  • 193
  • 1
  • 5

2 Answers2

3

The activation function you are using is not differentiable, because it has a step at every half-integer value of $x$. This could be a problem for training.

I would expect a better result using the identity as the activation function.

Other possible causes could be too small number of epochs or too small batch size. Your chosen value $1$ means Stochastic Gradient Descent, whose convergence tends to be more chaotic.

However, the weights you get aren't too far from the expected $w_1=w_2=1$, and their average is very close to it, so it looks like the code is probably right.

Jaume Oliver Lafont
  • 876
  • 7
  • 16
1

I advise to change the cost function to a mean squared error (as commonly done in regression problems): $\mathcal L(y,\hat{y}) = \frac{1}{2B}\sum_{i=0}^{B-1} (y^{(i)}-\hat{y}^{(i)})^2$; where you average the squared differences over the batch size $B$. Also it's common practice to divide by $1/2$ to remove the factor of $2$ when taking the derivative of this.

Moreover, since the range of the data can vary a lot, use some weight decay to reduce the magnitude of the weights and prevent over-fitting to a given range of values: this may also help to reach the optimal of $w_1=w_2 = 1$.

Finally, prefer larger batch sizes (e.g. 64, 128, ...) since the noise in the gradient reduces, and generate at least 20x more data samples.

Luca Anzalone
  • 3,216
  • 4
  • 15