Yes, but as the other answers said, the raw softmax output has the issue of overconfidence. So, you need a transformation to make them linear like logarithmic scale.
Logarithms have a unique relationship with infinity. As numbers approach infinity, logarithms grow, but they do so more slowly than the numbers themselves. This slow growth can be philosophically interpreted as a metaphor for how small actions or small steps can still have an infinite impact over time. The logarithm provides a bridge between the finite (real-world measurements like IEEE 754 representation) and the infinite (theoretical concepts), suggesting that even seemingly small, finite changes can have profound, infinite consequences.
To address the overconfidence issue, let $a$ be the maximum value of probability. Intuitively, putting them inside a logarithmic scale $ -\log_2(1 - a)$ would reduce the overconfidence issue as it's sensitive to the small difference when the $a$ close to $1$, therefore it can be used for confidence measurement.
Additionally, we can also consider the minimum value of probability to represent how assertive the softmax output's statement is as the support, and so that I can consider it as an uncertainty measurement.
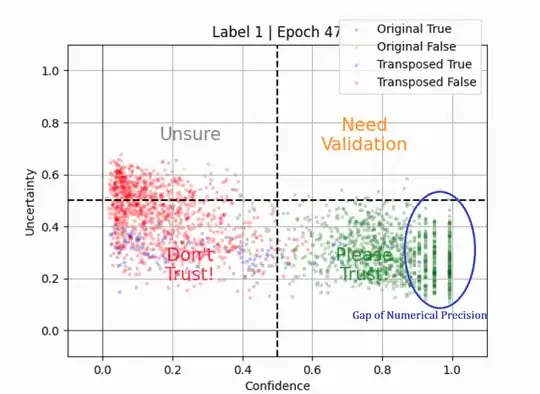
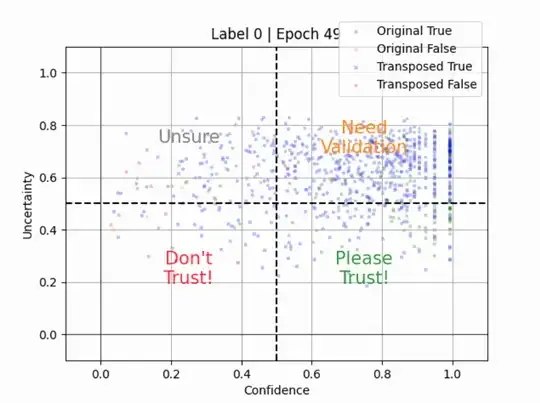
I tested it when I trained MNIST Handwritten Digit of 10 classes as usual. Where I use the original input and its 90-degree-rotated (transposed) input. Subjectively speaking, there is no such number that looks like a horizontal line for the class of digit number 1 when it's rotated while the class of digit number 0 is similar like its original when it's rotated.

Performing a transformation of raw softmax output into a logarithmic scale would produce probabilities of I don't know vs. I know, like this class of digit number 1 below. Notice that there are gaps of numerical precision, as the most real number is represented by IEEE 754 in most computers, which has limited precision.
Same for the class of digit number 0 below as expected, it is mostly correct to predict its rotated version as it's similar to the original.
Here is the full formula:
Inputs:
- Let $\mathbf{p} \in \mathbb{R}^{n_{\text{samples}} \times n_{\text{classes}}}$ be the input matrix of predicted probabilities, where:
- $n_{\text{samples}}$ is the number of samples.
- $n_{\text{classes}}$ is the number of classes (i.e., the number of possible predictions per sample).
- Each element $p_{i,j} \in [0, 1]$ represents the predicted probability for sample $i$ and class $j$, and for each $i$, we have $\sum_{j=1}^{n_{\text{classes}}} p_{i,j} = 1$.
Definitions:
- Let $N = n_{\text{classes}}$ denote the number of classes.
- Let $\text{inf} = -\log_2(\epsilon)$ (where $\epsilon$ is the smallest representable number for the input's data type)
- For each sample $i$, define:
- The maximum predicted probability $a_i = \max_j (p_{i,j})$.
- The minimum predicted probability $b_i = \min_j (p_{i,j})$.
Confidence:
For each sample $i$, the confidence is defined as:
$$
c_i = \log_2(N - 1) - \log_2(N) - \log_2(1 - a_i)
$$
where $a_i = \max_j (p_{i,j})$ is the maximum predicted probability for sample $i$.
Specifically:
The confidence for each sample is normalized as:
$$
c_i' = \frac{c_i}{\inf}
$$
where $\inf$ is a large constant, representing the inverse of the smallest representable number of the data type, ensuring that the confidence is mapped to the range $[0, 1]$.
Uncertainty:
The uncertainty for each sample $i$ is defined as:
$$
u_i = -\log_2(N) - \log_2(b_i) - c_i
$$
where $b_i = \min_j (p_{i,j})$ is the minimum predicted probability for sample $i$, and $c_i$ is the confidence for sample $i$.
Specifically:
The uncertainty for each sample is normalized as:
$$
u_i' = \frac{u_i}{\inf}
$$
where $\inf$ is the same large constant used for normalizing the confidence.
Then, the uncertainty is transformed as:
$$
u_i'' = \frac{2^{u_i'} - 1}{2^{u_i'} + 1}
$$
This maps the uncertainty values to the range $[0, 1]$.
Outputs:
- The output consists of two arrays:
- Confidence array $\mathbf{c}$: A normalized confidence value for each sample, where $c_i' \in [0, 1]$.
- Uncertainty array $\mathbf{u}$: A normalized uncertainty value for each sample, where $u_i'' \in [0, 1]$.
The final output is a matrix $\mathbf{output} \in \mathbb{R}^{n_{\text{samples}} \times 2}$, where each row contains the normalized confidence and uncertainty values for each sample.
Summary
So, you can say that the softmax output can represent the probability, except it represents the probability of I don't know this sample vs. I know this sample.


