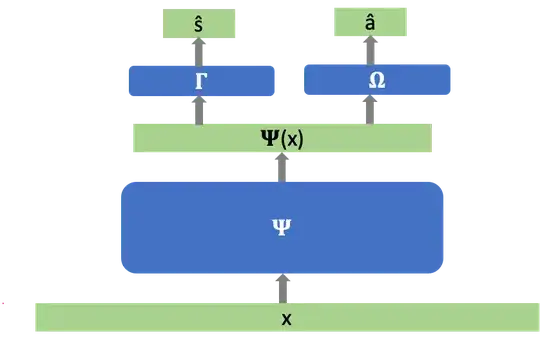
I need my model to predict $s$ from my data $x$. Additionally, I need the model to not use signals in $x$ that are predictive of a separate target $a$. My approach is to transform $x$ into a representation $\Psi(x)$ such that it's good at predicting $s$ but bad at predicting $a$.
Concretely, let the prediction for $s$ be \begin{equation} \hat{s} = (\Gamma \circ \Psi)(x), \end{equation} and that for $a$ be $$\hat{a} = (\Omega \circ \Psi)(x),$$ where $\Psi, \Gamma, \Omega$ are implemented as MLP layers. Further, let $\ell_s(\Psi,\Gamma)$ and $\ell_a(\Psi,\Omega)$ be the loss functions corresponding to $s$ and $a$, respectively.
The objective thus is to simultaneously
- minimize $$\ell_s(\Psi,\Gamma)$$ (good at predicting $s$), and
- maximize $$\min_\Omega \ell_a(\Psi,\Omega) := -f(\Psi)$$ (bad at predicting $a$)
There may not exist a $(\Psi, \Gamma)$ combination that simultaneously achieves both. So the hope is to find something on the Pareto frontier by linearly combining the objectives:
\begin{equation}
\tag{*}\label{*}
\min_{\Psi, \Gamma} \left[ \ell_s(\Psi,\Gamma) + \alpha f(\Psi) \right]
= \min_{\Psi, \Gamma} \left[ \ell_s(\Psi,\Gamma) - \alpha \min_\Omega \ell_a(\Psi,\Omega) \right]
\end{equation}
where $\alpha > 0 $ is a hyperparameter that trades off the two original objectives.
However, I'm not sure how to train the layers $\Psi, \Gamma, \Omega$ to achieve \eqref{*}.
One procedure I could think of is to alternate between
- Freeze $\Psi, \Gamma$ and tune $\Omega$ to minimize $\ell_a(\Psi,\Omega)$,
- Freeze $\Omega$ and tune $\Psi, \Gamma$ to minimize $\ell_s(\Psi,\Gamma) - \alpha \ell_a(\Psi,\Omega)$
until convergence. Would that work?
