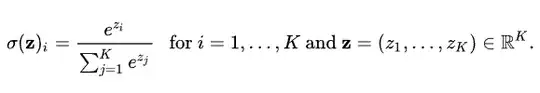2

I'm trying to understand this tutorial for Jax.

Here's an excerpt. It's for a neural net that is designed to classify MNIST images:

from jax.scipy.special import logsumexp

def relu(x):
  return jnp.maximum(0, x)


def predict(params, image):


per-example predictions


activations = image
  for w, b in params[:-1]:
    outputs = jnp.dot(w, activations) + b
    activations = relu(outputs)


final_w, final_b = params[-1]
  logits = jnp.dot(final_w, activations) + final_b
  return logits - logsumexp(logits)

I don't understand why they would subtract a constant value from all the final predictions, given that the only thing that matters is their relative values.

For clarity, here's the loss function:

def loss(params, images, targets):
  preds = batched_predict(params, images)
  return -jnp.mean(preds * targets)
nbro
  • 42,615
  • 12
  • 119
  • 217
Foobar
  • 153
  • 6

2 Answers2

2

Though I may be answering this question quite late, I would like to address your inquiry (because it's possible that other individuals may also have similar queries. :D)

You can think of the last 3 lines of the function predict as implementing a softmax layer. In this case, the function returns the log probability rather than the probability.

enter image description here

To be specific, logits stores $z_i=\ln{e^{z_i}}$ and logsumexp(...) computes the $\ln\sum_{j=1}^{K}{e^{z_j}}$. The returned value is thus $\ln{z_i} - \ln\sum_{j=1}^{K}{e^{z_j}} = \ln{ \frac{e^{z_i}}{\sum_{j=1}^{K}{e^{z_j}}}}$.

present42
  • 36
  • 2
1

It's apparently for numerical stability. From the Wikipedia page for LogSumExp:

A common purpose of using log-domain computations is to increase accuracy and avoid underflow and overflow problems when very small or very large numbers are represented directly (i.e. in a linear domain) using limited-precision floating point numbers.

And this answer from stats.stackexchange.com:

This is a simple trick to improve the numerical stability. As you probably know, exponential function grows very fast, and so does the magnitude of any numerical errors. This trick is based on [...]

That said, I'm not sure why it's required in your example because, unless I'm missing something, there is no exponential function which could introduce the aforementioned numerical instability.

I guess it's possible that it's a mistake in the JAX docs, but it seems more likely that I just don't understand it. Hopefully someone else will be able to comment/answer to provide an explanation. I figured I'd post this half-answer since there are no others answers here.

joe
  • 111
  • 2