Determining to terminate at a reward or not

Question

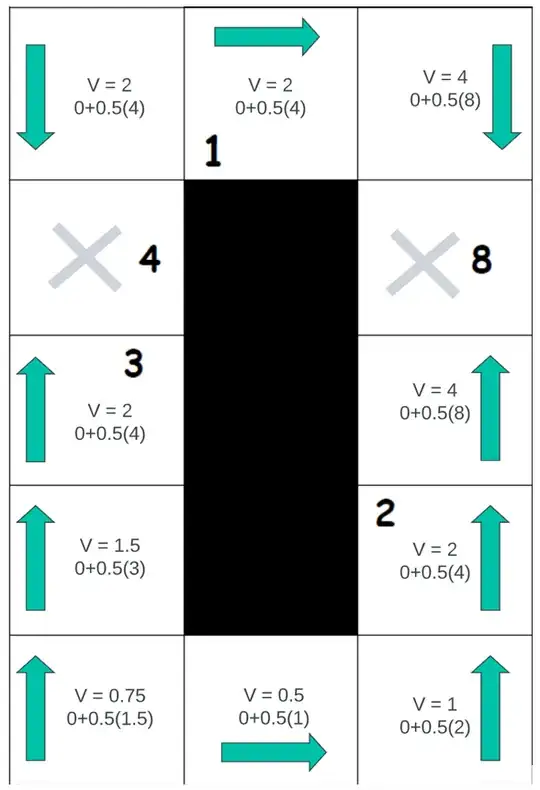
I am practicing the Bellman equation on Grid world examples and in this scenario, there are numbered grid squares where the agent can choose to terminate and collect the reward equal to the amount inside the numbered square or they can choose to not do this and just move to the state grid square.

Since this is a determinisitc grid, I have utilised the following Bellman equation: $$V(s) = max_a(R(s,a)+\gamma V(s'))$$

Where $\gamma=0.5$ and any movement reward is $0$, since this will allow the agent to have a balance of thinking long-term and short-term.

I am trying to understand how you would determine whether it is better for the agent to terminate at the state with the number $3$ or to continue to the state with a number $4$ to collect the more reward? I have determined and marked (X) the terminal states, where with my current calculations, I feel the agent should exit.

Answer 1

I am trying to understand how you would determine whether it is better for the agent to terminate at the state with the number 3 or to continue to the state with a number 4 to collect the more reward?

Which is better is determined by looking at the expected return from either choice, with higher expected returns being better.

The return from travelling one time step to the "4 on exit" state, is 2 as you have shown, due to discounting. That is assuming the 4 is gained by taking a separate "exit" action once in that position. That is, there is no combined "move and exit" action that only takes one time step - whether or not such actions exist in this environment makes a large change to your example and what will be optimal, so it is really important to be clear about that.

The return from exiting immediately in the "3 on exit" state is 3.

3 is larger than 2, so if the agent finds itself in the "3 on exit" state, then it should exit immediately to get the best expected return.

Possibly what might be making this harder to understand is the role that discounting takes. Sometimes it appears to be used to "fix" infinite rewards from continuing environments. However, discounting is part of the definition of return, and it changes what counts as optimal. With a low discount factor, such as $0.5$, then it can be optimal to take a lower reward sooner as opposed to a larger reward later. The value of the discount factor allows to make that comparison exactly.