Is the initialisation of $V(s)$ and $\pi(s)$ really arbitrary in policy iteration?

Question

In Sutton and Barto's book (Reinforcement learning: An introduction. MIT press, 2018), the algorithm "Policy Iteration" is:

Here, $V(s)$ is initialized arbitrarily, meaning that I can choose anything I want. Moreover, I think nothing is stated about $\gamma$ here so we can consider undiscounted environments where $\gamma = 1$. Now suppose we use the following environment:

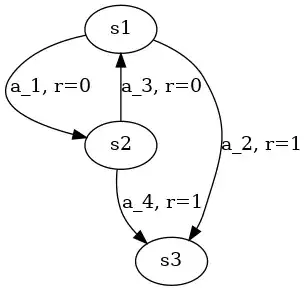
If I initialize:

• $V(s_1) = 10$
• $V(s_2) = 10$
• $V(s_3) = 0$
• $\pi(s_1) = a_1$
• $\pi(s_2) = a_3$

With this, it appears that the "Policy Evaluation" part will not have any effect and the algorithm will immediately stops, outputing a policy where the optimal actions are $\pi(s_1) = a_1$ and $\pi(s_2) = a_3$. What am I missing ?

---

EDIT: I made a toy repository to reproduce, if you want to tweak the numbers of point out something I misunderstood: https://github.com/Gregwar/policy_iteration_initialization/blob/master/policy_iteration.py

Answer 1

I think you have constructed a bad case for the algorithm as given. You have created an infinite loop and set starting values such that there is no chance for the loop to break out. You have also deliberately set up a starting policy for an episodic problem where the episode cannot terminate.

One simple rule to avoid this is to set $\pi$ to the stochastic equiprobable policy initially (i.e. the first policy will explore all edges of the MDP, making it very hard - maybe impossible - to construct bad cases), and all initial $V$ to $0$. Although these can be set arbitrarily, it is not the user of the solver that normally gets to decide these initialisations, but the person implementing the solver.

So, yes, the algorithm as shown does let you deliberately break it through apparently free choices that are not covered in the book. However, these look like edge cases that were maybe not worth covering in detail. The algorithm works if you pick reasonable arbitrary choices, but defining "reasonable" is fiddly and might distract from the introduction to the topic.