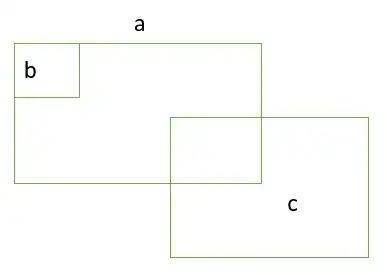
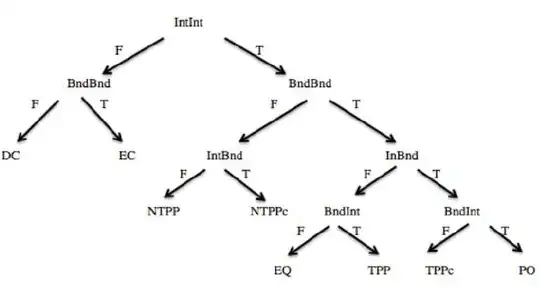
I am trying to use RCC8 algebra relations and axioms in order to tackle the following problem :
We consider the below configuration and square $x$ such that "$x$ NTPP $a$" and "$x$ TPP $c$"
and we must prove that :
- a) $x$ DC $b$
- b) For $y$ such that "$y$ EC $a$", prove that it is not possible to have "$y$ EC $x$"
using the tree
My difficulty is that I do not know how to "formally" prove the above statements using the tree.
For instance, regarding question (a), since "$x$ TPP $c$" and "$c$ DC $b$", by the composition table we have that "$x$ DC $b$". But, this argument does not use "Interior" and "Boundary" statements as the tree suggests. Could you please assist with this ?