I am currently doing research work on an inversion of geophysical data using Machine Learning. I have come across some research work where a Convolutional Neural Network (CNN) has been used effectively for this purpose (for example, his).
I am particularly interested in how to prepare my input and output labelled data for this machine learning application, since the input will be the observed geophysical signal, and the label output will be the causative density or susceptibility distribution (for gravity and magnetic, respectively).
I need some assistance and insight as to how to prepare the data for this CNN application.
Additional Explanation
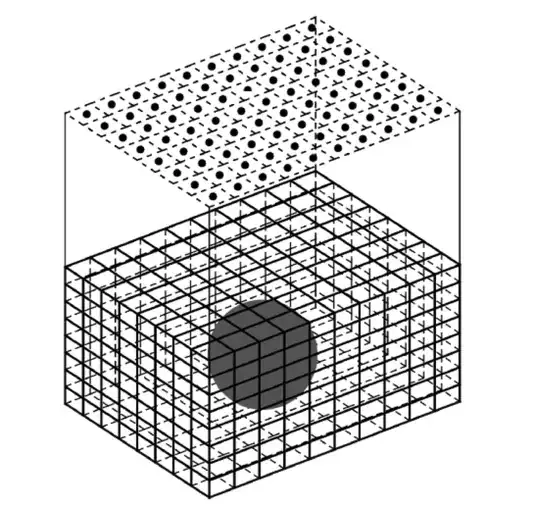
Experimental setup: Measurements are taking above the ground surface. These measurements are signals that reflect the distribution of a physical property (e.g., density) in the ground beneath. For modelling, the subsurface is discretised into squares or cubes each having a constant but unknown physical property (e.g., density).
How it applies to CNN: I want my input data to be the Measurements taken above ground. The output should then be the causative density distribution (that is, the value of the density in each cube/squares)
See attached picture (flat top is the "above ground", all other prisms represent the discretisation of the subsurface. I want to train the CNN to give out a density value for each cube in the subsurface, given the above ground measurements)