1

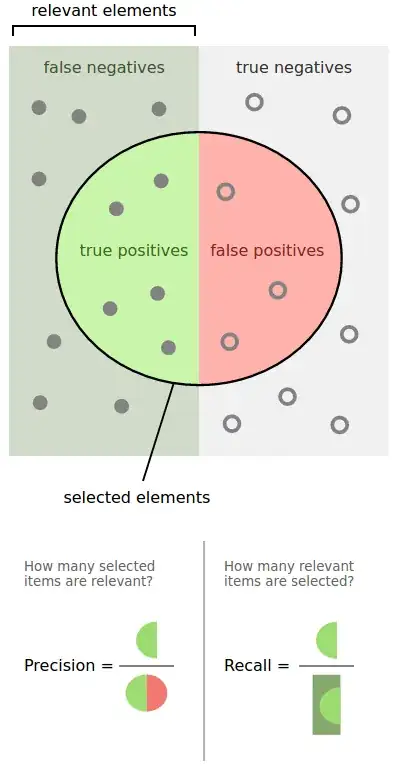
I'm attempting to develop a genetic algorithm capable of discovering classification rules for a given data set, a number of papers make use of the confidence (precision) and coverage of a rule to define its fitness. In particular, I've been following this paper.

However, I'm not sure my understanding of the equations is correct.

In that paper, the confidence is defined as

$$\text{conf} = \frac{|P \land D|}{|P|}$$

They describe it as follows

In classification problems, confidence measure is defined as the ratio of the number of examples in P that are correctly classified as decision class of D and the number of examples in P.

Is this saying the total number of occurrences of the attributes in a given rule $P$ which occur in rules which have been classified as class $D$, by the number of attributes in $P$?

Where an example of a rule containing two attributes would be as follows:

(martial_status = married & age > 30)

It seems a number of papers define it differently which has led to my confusion, if anyone is able to confirm my understanding or provide an some insight that'd be great.

nbro
  • 42,615
  • 12
  • 119
  • 217
Astronought
  • 189
  • 4

1 Answers1

1

The confidence equation you are referring to is the definition of precision in the Classification/pattern-recongition/information-retrieval contexts. You can visually understand the equation with the help of the following figure from the wikipedia page:

Visual representation of Precision which you interchangeably with confidence

 P     : Refers to the set of samples in your dataset. (Selected elements)
|P|    : Refers to the number of samples in your dataset.
 D     : Refers to the set of correct class labels.(aka. Ground Truth).
|P & D|: Refers to the number of samples in the dataset that the classifier correctly labeled.

I hope with this understanding you can implement the fitness function for your Genetic Algorithm. If you want more help in defining the fitness function, then you should probably add details about your approach or links to the research paper you are trying to follow.

PraveenPalanisamy
  • 141
  • 2