What does it mean by strong or sufficient gradient for training in this context?

Question

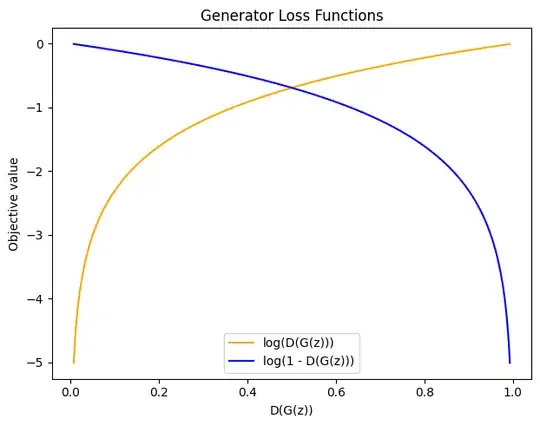
It has been mentioned in the research paper titled Generative Adversarial Nets that generator need to maximize the function $\log D(G(z))$ instead of minimizing $\log(1 −D(G(z)))$ since the former provides sufficient gradient than latter.

$$\min_G \max_DV(D, G) = \mathbb{E}_{x ∼ P_{data}}[\log D(x)] + \mathbb{E}_{z ∼ p_z}[log (1 - D(z))]$$ In practice, the above equation may not provide sufficient gradient for $G$ to learn well. Early in learning, when $G$ is poor, $D$ can reject samples with high confidence because they are clearly different from the training data. In this case, $\log(1 −D(G(z)))$ saturates. Rather than training $G$ to minimize $\log(1 −D(G(z)))$ we can train G to maximize $\log D(G(z))$. This objective function results in the same fixed point of the dynamics of $G$ and $D$ but provides much stronger gradients early in learning.

A gradient is a vector containing the partial derivatives of outputs w.r.t inputs. At a particular point, the gradient is a vector of real numbers. These gradients are useful in the training phase by providing direction-related information and the magnitude of step in the opposite direction. This is my understanding regarding gradients.

What is meant by sufficient or strong gradient? Is it the norm of the gradient or some other measure on the gradient vector?

If possible, please show an example of strong and weak gradients with numbers so that I can quickly understand.

Answer 1

The terms "insufficient gradient" or "not strong enough gradient" usually means that the magnitude of the gradient vector is too small or nearly zero that they can't drive the optimization properly.

Not having sufficient gradient is similar to having a very low learning rate - they are not only slow (in terms of convergence) but also drifts the optimization in a poor direction and get stuck in local minima.

Answer 2

As mentioned by @ayandas answer, we care about the magnitude of the gradient to define the speed of learning. When we have a saturated region (in 2D, it is an almost horizontal curve), then the gradient is almost zero, and the training will be slow.

You can try to mitigate that with an adaptive learning rate. But in the paper, they just maximize a different objective.

I have attached graphs of both functions, You can notice that in the region near zero on the x-axis (the region we will be in early in training), the original objective is almost flat with gradients of almost zero. On the other hand, the new objective is much better with a gradient magnitude of almost 1.