Does gradient descent in deep learning assume a smooth fitness landscape?

Question

I've come across the concept of fitness landscape before and, in my understanding, a smooth fitness landscape is one where the algorithm can converge on the global optimum through incremental movements or iterations across the landscape.

My question is: Does deep learning assume that the fitness landscape on which the gradient descent occurs is a smooth one? If so, is it a valid assumption?

Most of the graphical representations I have seen of gradient descent show a smooth landscape.

This Wikipedia page describes the fitness landscape.

Answer 1

I'm going to take the fitness landscape to be the graph of the loss function, $\mathcal{G} = \{\left(\theta, L(\theta)\right) : \theta \in \mathbb{R}^n\}$, where $\theta$ parameterises the network (i.e. it is the weights and biases) and $L$ is a given loss function; in other words, the surface you would get by plotting the loss function against its parameters.

We always assume the loss function is differentiable in order to do backpropagation, which means at the very least the loss function is smooth enough to be continuous, but in principle it may not be infinitely differentiable¹.

You talk about using gradient descent to find the global minimiser. In general this is not possible: many functions have local minimisers which are not global minimisers. For an example, you could plot $y = x^2 \sin(1/x^2)$: of course the situation is similar, if harder to visualise, in higher dimensions. A certain class of functions known as convex functions satisfy the property that any local minimiser is a global minimiser. Unfortunately, the loss function of a neural network is rarely convex.

For some interesting pictures, see Visualizing the Loss Landscape of Neural Nets by Li et al.

---

¹ For a more detailed discussion on continuity and differentiability, any good text on mathematical analysis will do, for example Rudin's Principles of Mathematical Analysis. In general, any function $f$ that is differentiable on some interval is also continuous, but it need not be twice differentiable, i.e. $f''$ need not exist.

Answer 2

Main answer

To answer your question as directly as possible: No, deep learning does not make that "assumption".

But you're close. Just swap the word "assumption" with "imposition".

Deep learning sets things up such that the landscape is (mostly) smooth and always continuous*, and therefore it is possible to do some sort of optimization via gradient descent.

* quick footnotes on that bit:

• Smoothness is a stronger condition than continuity, that's why I mention them both.
• My statement is not authoritative, so take it with a grain of salt, especially the "always" bit. Maybe someone will debunk this in the comments.
• The reason that I say "(mostly) smooth" is because I can think of a counter example to smoothness, which is the ReLU activation function. ReLU is still continuous though.

Further elaboration

In deep learning we have linear layers which we know are differentiable. We also have non-linear activations, and a loss function which for the intents of this discussion can be bundled with non-linear activations. If you look at papers which focus specifically on crafting new types of non-linear activations and loss functions you will usually find a discussion section that goes something like "and we designed it this way such that it's differentiable. Here's how you differentiate it. Here are the properties of the derivative". For instance, just check out this paper on ELU, a refinement on ReLU.

We don't need to "assume" anything really, as we are the ones who designate the building blocks of the deep learning network. And the building blocks are not all that complicated in themselves, so we can know that they are differentiable (or piecewise differentiable like ReLU). And for rigor, I should also remind you that the composition of multiple differentiable functions is also differentiable.

So hopefully that helps you see what I mean when I say deep learning architects "impose" differentiability, rather than "assume" it. After all, we are the architects!

Answer 3

Does deep learning assume that the fitness landscape on which the gradient descent occurs is a smooth one?

One can interpret this question from a formal-mathematical standpoint and from a more "intuitively-practical" standpoint.

From the formal point of view, smoothness is the requirement that the function is continuous with continuous first derivatives. And this assumption is quite often not true in lots of applications - mostly because of the widespread use of ReLU activation function - it is not differentiable at zero.

From the practical point of view, though, by "smoothness" we mean that the function's "landscape" does not have a lot of sharp jumps and edges like that:

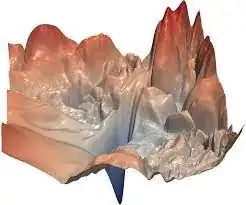
Practically, there's not much difference between having a discontinuous derivative and having derivatives making very sharp jumps.

And again, the answer is no - the loss function landscape is extremely spiky with lots of sharp edges - the picture above is an example of an actual loss function landscape.

But... why the gradient descent works then?

As far as I know, this is a subject of an ongoing discussion in the community. There are different takes and some conflicting viewpoints that are still subject of a debate.

My opinion is that, fundamentally, the idea that we need it to converge to the global optimum is a flawed one. Neural networks was shown to have enough capacity to completely remember the training dataset. A neural network, that completely remembered the training data. has reached the global optimization minimum (given only the training data). We are not interested in such overtrained models - we want models that generalize well.

As far as I know, there is no conclusive results on which properties of the minimum are linked to ability to generalize. People argued that these should be the "flat" minima, but then it was refuted. After that a "wide optimium" term was introduced and gave rise of an interesting technique of Stochastic Weight Averaging.