2

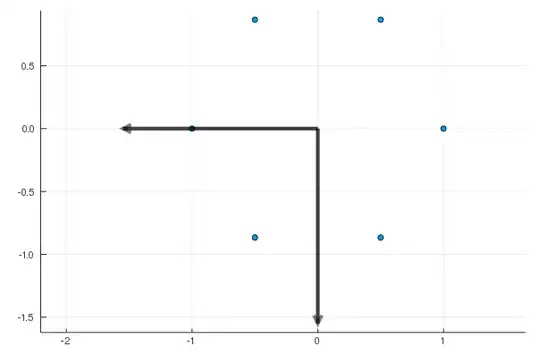
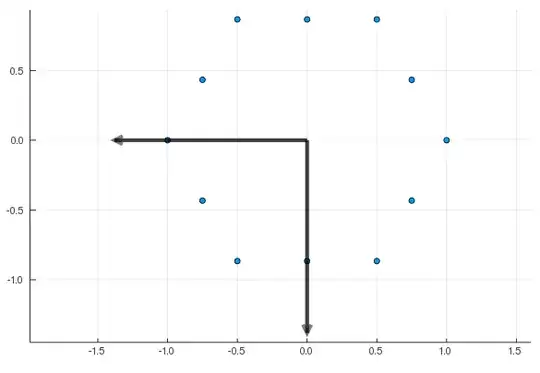
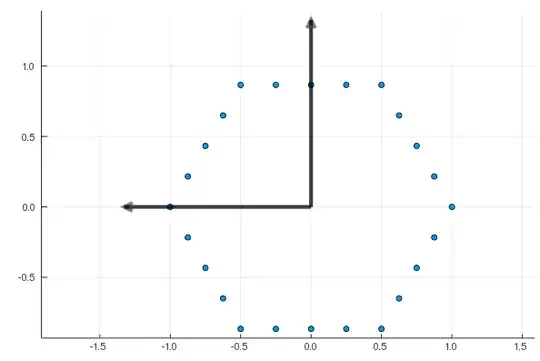
I do PCA on the data points placed in the corners of a hexagon, and get the following principal components:

enter image description here

The PCA variance is $0.6$ and is the same for each component. Why is that? Shouldn't it be greater in the horizontal direction than in the vertical direction? The data is between $-1$ and $1$ in the $x$-direction but only between $-\sqrt{3}/2$ and $\sqrt{3}/2$ in the $y$-direction. Why PCA results in the equal length components?

The length of each vector in the picture is the twice the square root of the variance.

UPDATE: added more points, the variances changed to $0.477$ but still they are equal.

enter image description here

UPDATE 2: Added even more points, the variances changed to $0.44$ but still they are equal.

enter image description here

Vladislav Gladkikh
  • 534
  • 6
  • 14

1 Answers1

3

Assuming that the $6$ vertices of the hexagon are on the unit circle,

>>> from sympy import *
>>> A = Matrix([[ 1, Rational(1,2),-Rational(1,2), -1, -Rational(1,2), Rational(1,2)], 
                [ 0,     sqrt(3)/2,     sqrt(3)/2,  0,     -sqrt(3)/2,    -sqrt(3)/2]])
>>> A * A.T
Matrix([[3, 0],
        [0, 3]])

Since ${\bf A} {\bf A}^\top - 3 \, {\bf I}_2 = {\bf O}_2$, any two orthogonal directions could be the principal components.

Rodrigo de Azevedo
  • 168
  • 7