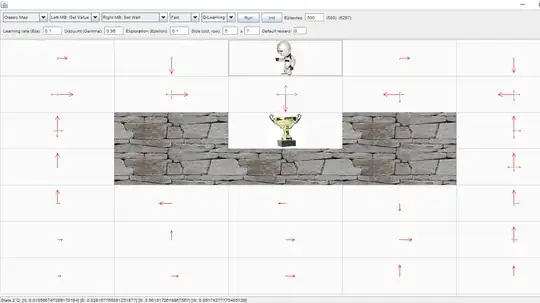
I am currently trying to learn reinforcement learning and I started with the basic gridworld application. I tried Q-learning with the following parameters:
- Learning rate = 0.1
- Discount factor = 0.95
- Exploration rate = 0.1
- Default reward = 0
- The final reward (for reaching the trophy) = 1
After 500 episodes I got the following results:
How would I compute the optimal state-action value, for example, for state 2, where the agent is standing, and action south?
My intuition was to use the following update rule of the $q$ function:
$$Q[s, a] = Q[s, a] + \alpha (r + \gamma \max_{a'}Q[s', a'] — Q[s, a])$$
But I am not sure of it. The math doesn't add up for me (when using the update rule).
I am also wondering either I should use the backup diagram to find the optimal state-action q value by propagating the reward (gained from reaching the trophy) to the state in question.
For reference, this is where I learned about the backup diagram.