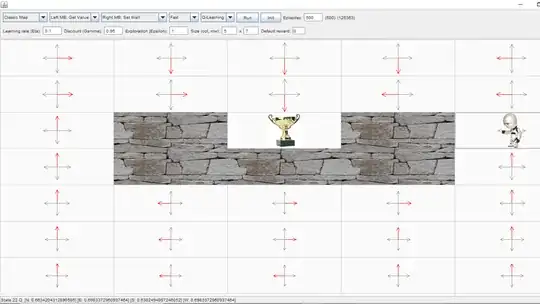
I am working on this assignment where I made the agent learn state-action values (Q-values) with Q-learning and 100% exploration rate. The environment is the classic gridworld as shown in the following picture.
Here are the values of my parameters.
- Learning rate = 0.1
- Discount factor = 0.95
- Default reward = 0
Reaching the trophy is the final reward, no negative reward is given for bumping into walls or for taking a step.
After 500 episodes, the arrows have converged. As shown in the figure, some states have longer arrows than others (i.e., larger Q-values). Why is this so? I don't understand how the agent learns and finds the optimal actions and states when the exploration rate is 100% (each action: N-S-E-W has 25% chance to be selected)