This is a topic I have been arguing about for some time now with my colleagues, maybe you could also voice your opinion about it.
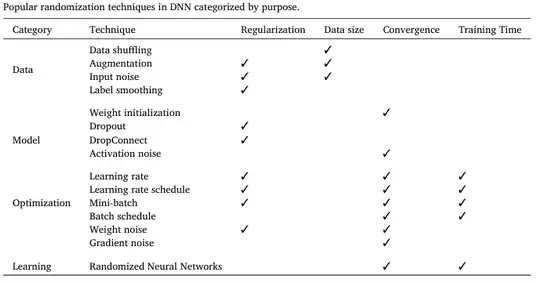
Artificial neural networks use random weight initialization within a certain value range. These random parameters are derived from a pseudorandom number generator (Gaussian etc.) and they have been sufficient so far.
With a proper sample simple, pseudorandom numbers can be statistically tested that they are in fact not true random numbers. With a huge neural network like GPT-3 with roughly 175 billion trainable parameters, I guess that if you would use the same statistical testing on the initial weights of GPT-3 you would also get a clear result that these parameters are pseudorandom.
With a model of this size, could in theory at least the repeatable structures of initial weights caused by their pseudorandomness affect the model fitting procedure in a way that the completed model would be affected (generalization or performance-wise)? In other words, could the quality of randomness affect the fitting of huge neural networks?