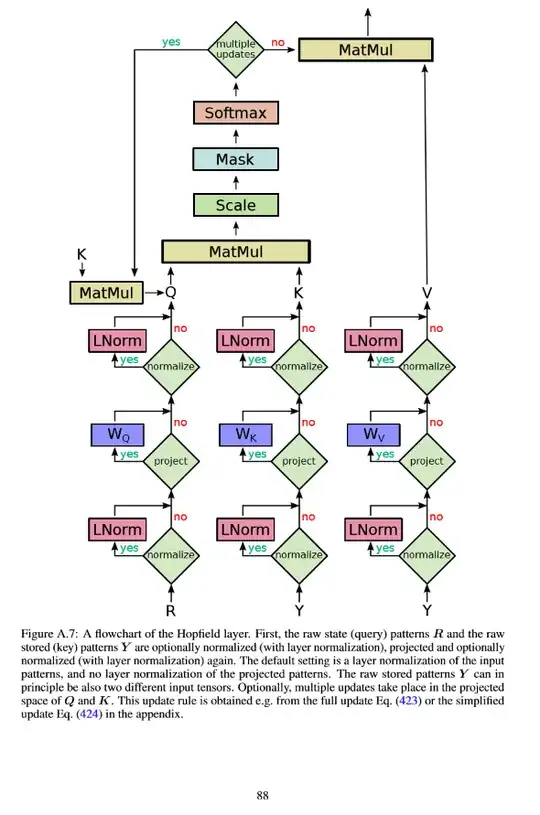
In the paper Hopfield networks is all you need, the authors mention that their modern Hopfield network layers are a good replacement for pooling, GRU, LSTM, and attention layers, and tend to outperform them in various tasks.
I understand that they show that the layers can store an exponential amount of vectors, but that should still be worse than attention layers that can focus parts of an arbitrary length input sequence.
Also, in their paper, they briefly allude to Neural Turing Machine and related memory augmentation architectures, but do not comment on the comparison between them.
Has someone studied how these layers help improve the performance over pooling and attention layers, and is there any comparison between replacing layers with Hopfield layers vs augmenting networks with external memory like Neural Turing Machines?
Edit 29 Jan 2020 I believe my intuition that attention mechanism should outperform hopfield layers was wrong, as I was comparing the hopfield layer that uses an input vector for query $R (\approx Q)$ and stored patterns $Y$ for both Key $K$ and Values $V$. In this case my assumption was that hopfield layer would be limited by its storage capacity while attention mechanism does not have such constraints.
However the authors do mention that the input $Y$ may be modified to ingest two extra input vectors for Key and Value. I believe in this case it would perform hopfield network mapping instead of attention and I do not know how the 2 compare.