10

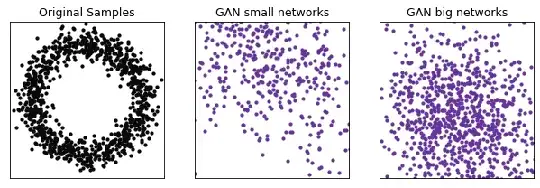
I am working with generative adversarial networks (GANs) and one of my aims at the moment is to reproduce samples in two dimensions that are distributed according to a circle (see animation). When using a GAN with small networks (3 layers with 50 neurons each), the results are more stable than with bigger layers (3 layers with 500 neurons each). All other hyperparameters are the same (see details of my implementation below).

I am wondering if anyone has an explanation for why this is the case. I could obviously try to tune the other hyperparameters to get good performance but would be interested in knowing if someone has heuristics about what is needed to change whenever I change the size of the networks.

GAN with smaller layer size reproduces the original samples better

Network/Training parameters

I use PyTorch with the following settings for the GAN:

Networks:

  • Generator/Discriminator Architecture (all dense layers): 100-50-50-50-2 (small); 100-500-500-500-2 (big)
  • Dropout: p=0.4 for generator (except last layer), p=0 for discriminator
  • Activation functions: LeakyReLU (slope 0.1)

Training:

  • Optimizer: Adam
  • Learning Rate: 1e-5 (for both networks)
  • Beta1, Beta2: 0.9, 0.999
  • Batch size: 50
hanugm
  • 4,102
  • 3
  • 29
  • 63
Mafu
  • 144
  • 5

1 Answers1

1

Variance

What it seems to be taking place here is a form of overfitting. Specifically when using larger layers, the model may become too complex and start to fit the noise in the training data, rather than the underlying patterns. This can lead to poor generalization performance and, as seen here unstable behavior.

Other

Other complexities that may arise when using larger layers is diversity issues. Specifically, more complex GAN models may produce less diverse output from the generator, as the network is prone to get stuck in a particular mode of the data distribution and fail to explore other areas.

To address this issue, regularisation techniques such as dropout or noise introduction can be deployed to encourage the generator to produce more diverse output. Additionally modifying the loss function can encourage the generator to explore different modes of the data distribution.

hH1sG0n3
  • 231
  • 1
  • 7