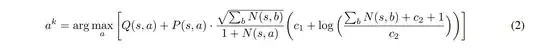8

From the AlphaGo Zero paper, during MCTS, statistics for each new node are initialized as such:

${N(s_L, a) = 0, W (s_L, a) = 0, Q(s_L, a) = 0, P (s_L, a) = p_a}$.

The PUCT algorithm for selecting the best child node is $a_t = argmax(Q(s,a) + U(s,a))$, where $U(s,a) = c_{puct} P(s,a) \frac{\sqrt{\sum_b N(s,b)}}{1 + N(s, a)}$.

If we start from scratch with a tree that only contains the root node and no children have been visited yet, then this should evaluate to 0 for all actions $a$ that we can take from the root node. Do we then simply uniformly sample an action to take?

Also, during the expand() step when we add an unvisited node $s_L$ to the tree, this node's children will also have not been visited, and we run into the same problem where PUCT will return 0 for all actions. Do we do the same uniform sampling here as well?

sb3
  • 167
  • 1
  • 7

2 Answers2

6

I looked at the Python pseudo-code attached to the Data S1 of the Supplementary Materials of the AlphaZero paper. Here is my findings:

  • Contrary to the paper, AlphaZero does not store $\{N(s, a), W(S, a), Q(s, a), P(s, a)\}$ statistics for each edge $(s,a)$. Instead, AlphaZero stores $\{N(s), W(S), Q(s), P(s)\}$ statistics for each node $s$.
  • When a leaf node $S_L$ is expanded, it's visit count, value scores, and action policies are immediately updated in $\{N(s), W(S), Q(s), P(s)\}$, so $N(s)$ is at least $1$. This is why in the paper, the backprop step updates for all time steps $t \le L$ rather than $t < L$. It makes sense to update $s_L$ even though there is no corresponding $a_L$ to pair it with.
  • Therefore, when a new leaf node is expanded, the value $U(s, a)$ of a child of that leaf node will be nonzero, since $\sqrt{\sum_b N(s,b)}$ is actually computed as $N(s_{parent})$ in the code, which is at least 1.
  • Oddly enough, I think there might be a bug in the pseudocode, because at the beginning on the first iteration (starting at the root node), $U(s,a) = 0$ for all child nodes of the root node. This is because at the first iteration, $N(s_{root}) = 0$. The value of all child nodes will be $0$, and since the authors chose to break ties according to Python's max function, the algorithm simply chooses the first element it finds in case of a tie.
  • After the first iteration, $N(s_{root}) > 0$ and so $U(s,a) \neq 0$ and things proceed as normal since the backprop step will have updated the visit count of the root node. So this possible bug/unintuitive behavior only affects the first iteration. It is extremely minor and insignificant, and does not affect the outcome of the MCTS, which is probably why it went unnoticed.
user3667125
  • 1,700
  • 9
  • 16
1

I had the same question and found this page, then I also started to look at the pseudo-code of Supplementary Materials. The code of the computation of the UCB score is as followed:

# The score for a node is based on its value, plus an exploration bonus based on
# the prior.
def ucb_score(config: AlphaZeroConfig, parent: Node, child: Node):
  pb_c = math.log((parent.visit_count + config.pb_c_base + 1) /
                  config.pb_c_base) + config.pb_c_init
  pb_c *= math.sqrt(parent.visit_count) / (child.visit_count + 1)

prior_score = pb_c * child.prior
  value_score = child.value()
  return prior_score + value_score

I was very confused since it is different from the formula described in the paper, until I found the UCB formula in the paper of MuZero:

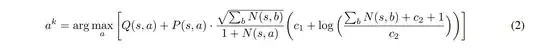
enter image description here

It is clear that the pseudocode of AlphaZero mistook the UCB formula of MuZero.

As for the original question, the sum of all the visit count numbers of the childen is implemented as the visit count of the parent node, which is at least 1, since it is visited as it is expanded (evaluated), as you can see in the code of the search:

# Core Monte Carlo Tree Search algorithm.
# To decide on an action, we run N simulations, always starting at the root of
# the search tree and traversing the tree according to the UCB formula until we
# reach a leaf node.
def run_mcts(config: AlphaZeroConfig, game: Game, network: Network):
  root = Node(0)
  evaluate(root, game, network)
  add_exploration_noise(config, root)

for _ in range(config.num_simulations):
    node = root
    scratch_game = game.clone()
    search_path = [node]


while node.expanded():
  action, node = select_child(config, node)
  scratch_game.apply(action)
  search_path.append(node)

value = evaluate(node, scratch_game, network)
backpropagate(search_path, value, scratch_game.to_play())



return select_action(config, game, root), root
leodeng
  • 11
  • 2