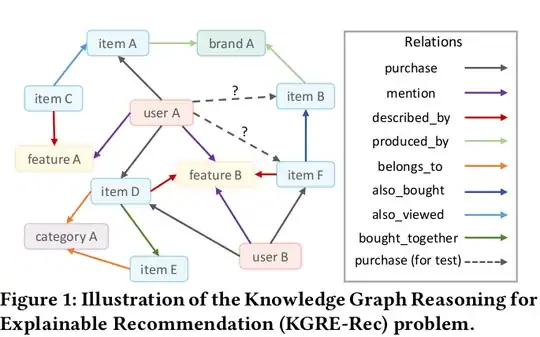
I've been reading this paper on recommendation systems using reinforcement learning (RL) and knowledge graphs (KGs).
To give some background, the graph has several (finitely many) entities, of which some are user entities and others are item entities. The goal is to recommend items to users, i.e. to find a recommendation set of items for every user such that the user and the corresponding items are connected by one reasoning path.
I'm attaching an example of such a graph for more clarity (from the paper itself) -
In the paper above, they say
First, we do not have pre-defined targeted items for any user, so it is not applicable to use a binary reward indicating whether the user interacts with the item or not. A better design of the reward function is to incorporate the uncertainty of how an item is relevant to a user based on the rich heterogeneous information given by the knowledge graph.
I'm not able to understand the above extract, which talks about the reward function to use - binary, or something else. A detailed explanation of what the author is trying to convey in the above extract would really help.