Generally, if one googles "quantum machine learning" or anything similar the general gist of the results is that quantum computing will greatly speed up the learning process of our "classical" machine learning algorithms.
This is correct. A lot of machine learning methods involve linear algebra, and it often takes far fewer quantum operations to do things in linear algebra than the number of classical operations that would be needed. To be more specific, for a matrix of size $N\times N$, if a classical computer needs $f(N)$ operations to do some linear algebra operation, such as diagonalization which can take $f(N)=\mathcal{O}(N^3)$ operations on a classical computer, a quantum computer would often need only $\log_2 f(N)$ operations, which inn (in and only in) the language of computational complexity theory, means exponential speed-up. The "only in" part is there because we have made here an assumption that "fewer quantum operations" means "speed-up", which for now is something we only know to be true in the world of "computational complexity theory".
However, "speed-up" itself does not seem very appealing to me as the current leaps made in AI/ML are generally due to novel architectures or methods, not faster training.
I disagree. Take vanilla deep learning for example (without GANs or any of the other things that came up in the last decade). Hinton and Bengio had been working on deep learning for decades, so why did interest in deep learning suddenly start growing so much from 2011-2014 after a roughly monotonic curve from 1988-2010? Not that this rise started before newer advances such as GANs and DenseNet were developed:
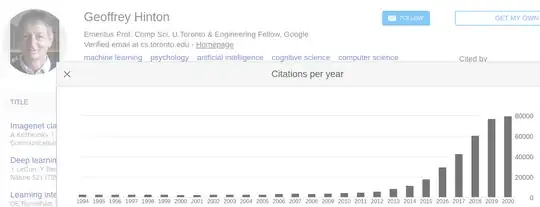
Notice also the similarity between the above graph and these ones:
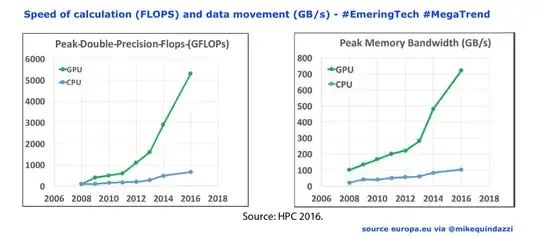
These days pretty much everyone doing deep learning uses GPUs if they have access to GPUs, and what is possible to accomplish is extremely tied to what computing power a group has. I don't want to undermine the importance of new methods and new algorithms, but GPUs did play a big role for at least some areas of machine learning, such as deep learning.
Are there any quantum machine learning methods in development that are fundamentally different from "classical" methods?
I think you mean: "Most quantum machine learning algorithms are simply based on classical machine learning algorithms, but with some sub-routine sped-up by the QPU instead of a GPU -- are there any quantum algorithms that are not based on classical machine learning algorithms, and are entirely different".
The answer is yes, and more experts might be able to tell you more here.
One thing you might consider looking at is Quantum Boltzmann Machines.
Another things I'll mention is that a child prodigy named Ewin Tang who began university at age 14, discovered at around the age of 17 some classical algorithms that were inspired by quantum algorithms rather than the other way around, and
the comments on the Stack Exchange question Quantum machine learning after Ewin Tang might give you more insight on that. This is related to something called dequantization of quantum algorithms.
By this I mean that these methods are (almost*) impossible to perform on "classical" computers. *except for simulation of the quantum computer of course
Unfortunately quantum computers can't do anything that's impossible for classical computers to do, apart from the fact that they might be able to do some things faster. Classical computation is Turing complete, meaning anything that can be computed can be computed on a big enough classical computer.

