I keep looking through the literature, but can't seem to find any information regarding the time complexity of the forward pass and back-propagation of the sequence-to-sequence RNN encoder-decoder model, with and without attention.
The paper Attention is All You Need by Vaswani et. al in 2017 states the forward pass cost is $O(n^3)$, which makes sense to me (with 1 hidden layer). In terms of $X$ the input length, and $Y$ the output length, it then looks like $O(X^3 + Y^3)$, which I understand.
However, for training, it seems to me like one back-propagation is at worst $O(X^3 + Y^3)$, and we do $Y$ of them, so $O(Y(X^3 Y^3))$.
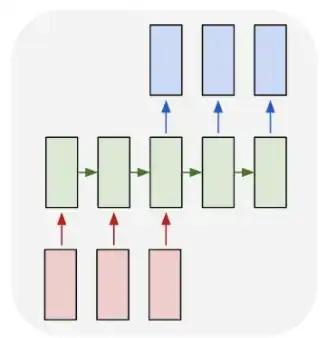
This is the following diagram, where the green blocks are the hidden states, the red ones are the input text and the blue ones are output text.
If I were to add global attention, as introduced by Luong et. al in 2015, the attention adds an extra $X^2$ in there due to attention multiplication, to make an overall inference of $O(X^3 + X^2 Y^3)$, and training even worse at $O(XY(X^3 + X^2 Y^3))$ since it needs to learn attention weights too.
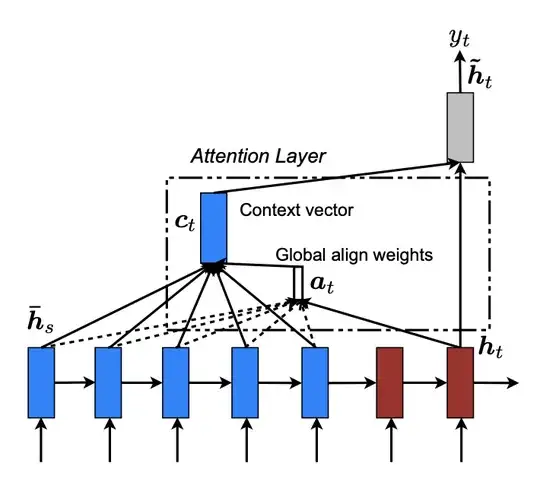
The following diagram shows the sequence-to-sequence model with attention, where $h$'s are the hidden states, $c$ is the context vector and $y$ is the output word, $Y$ of such output words and $X$ such inputs. This setup is described in the paper Effective Approaches to Attention-based Neural Machine Translation, by Luong et al. in 2015.
Is my intuition correct?