How to classify data which is spiral in shape?

Question

I have been messing around in tensorflow playground. One of the input data sets is a spiral. No matter what input parameters I choose, no matter how wide and deep the neural network I make, I cannot fit the spiral. How do data scientists fit data of this shape?

Answer 1

There are many approaches to this kind of problem. The most obvious one is to create new features. The best features I can come up with is to transform the coordinates to spherical coordinates.

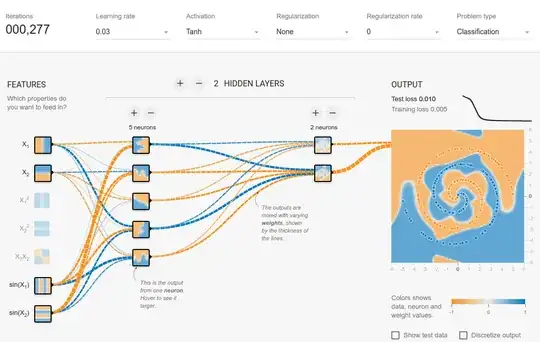
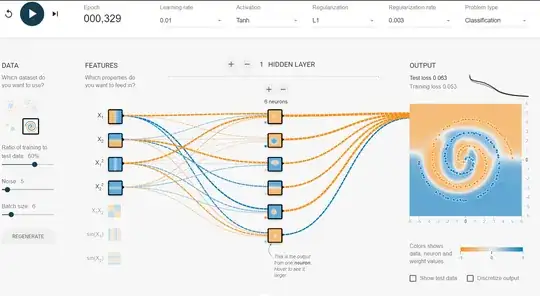
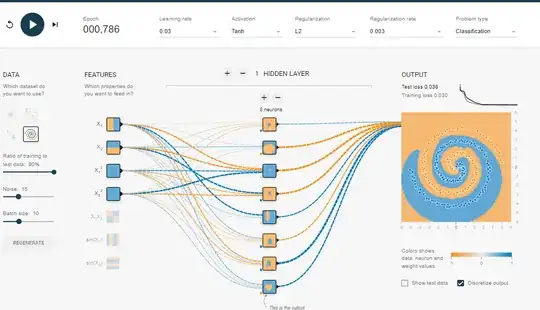
I have not found a way to do it in playground, so I just created a few features that should help with this (sin features). After 500 iterations it will saturate and will fluctuate at 0.1 score. This suggest that no further improvement will be done and most probably I should make the hidden layer wider or add another layer.

Not a surprise that after adding just one neuron to the hidden layer you easily get 0.013 after 300 iterations. Similar thing happens by adding a new layer (0.017, but after significantly longer 500 iterations. Also no surprise as it is harder to propagate the errors). Most probably you can play with a learning rate or do an adaptive learning to make it faster, but this is not the point here.

Answer 2

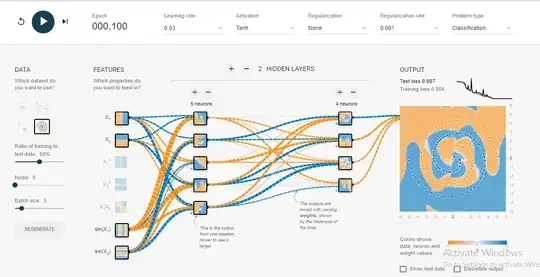
Ideally neural networks should be able to find out the function out on it's own without us providing the spherical features. After some experimentation I was able to reach a configuration where we do not need anything except $X_1$ and $X_2$. This net converged after about 1500 epochs which is quite long. So the best way might still be to add additional features but I am just trying to say that it is still possible to converge without them.

Answer 3

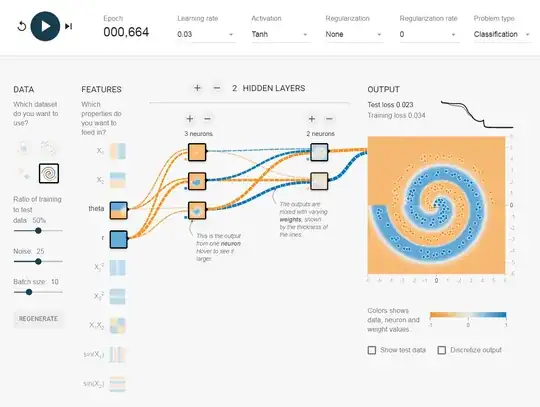
By cheating... theta is $\arctan(y,x)$, $r$ is $\sqrt{(x^2 + y^2)}$.

In theory, $x^2$ and $y^2$ should work, but, in practice, they somehow failed, even though, occasionally, it works.

Answer 4

You can increase no of hidden layers. Following is an example (But not very efficient)

Answer 5

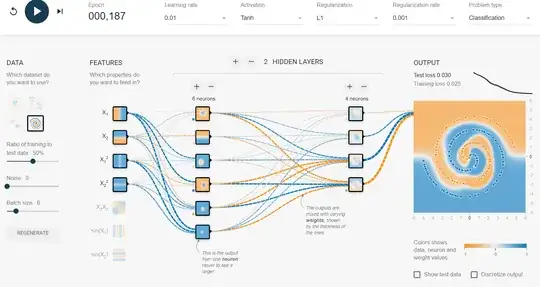
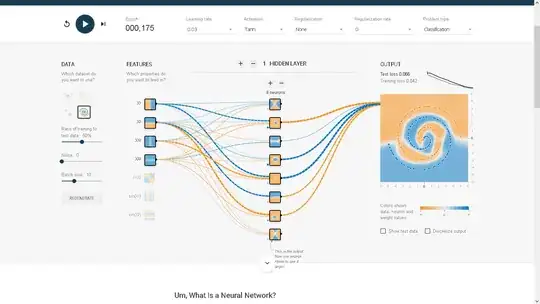
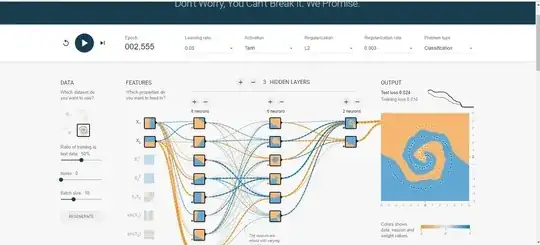
This is an example of vanilla Tensorflow playground with no added features and no modifications. The run for Spiral was between 187 to ~300 Epoch, depending. I used Lasso Regularization L1 so I could eliminate coefficients. I decreased the batch size by 1 to keep the output from over fitting. In my second example I added some noise to the data set then upped the L1 to compensate.

Answer 6

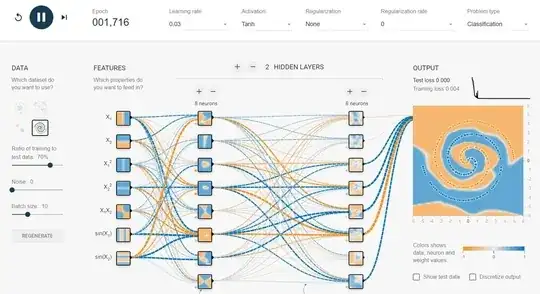
The solution I reached after an hour of trial usually converges in just 100 epochs.

Yeah, I know it does not have the smoothest decision boundary out there, but it converges pretty fast.

I learned a few things from this spiral experiment:-

• The output layer should be greater than or equal to the input layer. At least that's what I noticed in the case of this spiral problem.
• Keep the initial learning rate high, like 0.1 in this case, then as you approach a low test error like 3-5% or less, decrease the learning rate by a notch(0.03) or two. This helps in converging faster and avoids jumping around the global minima.
• You can see the effects of keeping the learning rate high by checking the error graph at the top right.
• For smaller batch sizes like 1, 0.1 is too high a learning rate as the model fails to converge as it jumps around the global minima.
• So, if you would like to keep a high learning rate(0.1), keep the batch size high(10) as well. This usually gives a slow yet smoother convergence.

Coincidentally the solution I came up with is very similar to the one provided by Salvador Dali.

Kindly add a comment, if you find any more intuitions or reasonings.

Answer 7

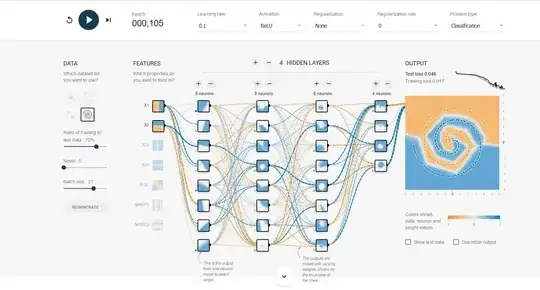
This is the architecture proposed and tested on the playground tensor flow for the Spiral Dataset. Two Hidden Layers with 8 neurons each is proposed with Tanh activation function.

Answer 8

May be you need reset all settings, and select x squared and y squared, only 1 hidden layer with 5 neurons.

Answer 9

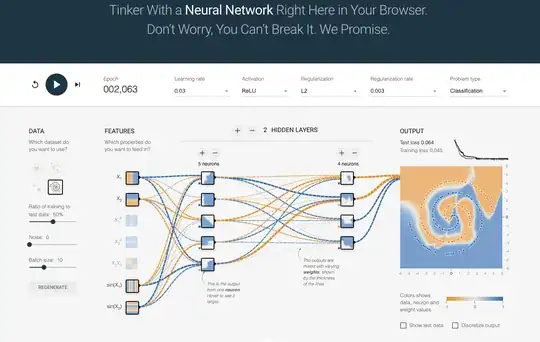I’ve experimented with multilayer perceptrons (MLPs) to understand their efficacy in handling complex, non-linear patterns like spirals. Here are some insights and configurations that I’ve found beneficial:

1.  Layer Configuration: Using multiple hidden layers helps in capturing the intricacies of spiral boundaries. Typically, starting with two layers and adjusting based on validation accuracy is a good approach.
2.  Neuron Distribution: Increasing the number of neurons in the first hidden layer and gradually reducing it in subsequent layers can effectively capture the finer details and variations in the data.
3.  Activation Functions: Non-linear activation functions like ReLU have shown promising results in enhancing model capabilities to learn complex patterns over traditional sigmoid functions, due to their ability to mitigate the vanishing gradient problem.
4.  Training Techniques: Employ techniques like batch normalization and dropout to improve generalization and prevent overfitting, which is crucial given the complex nature of spiral data.

Answer 10

May be you need reset all settings, only 1 hidden layer with 8 neurons, and 90% Dataset