How can I prove that gradient descent doesn't necessarily find the global optimum?
For example, consider the following function
$$f(x_1, x_2, x_3, x_4) = (x_1 + 10x_2)^2 + 5x_2^3 + (x_2 + 2x_3)^4 + 3x_1x_4^2$$
Assume also that we can't find the optimal value for the learning rate because of time constraints.
You can find by yourself a counterexample that, in general, GD is not guaranteed to find the global optimum!
I first advise you to choose a simpler function (than the one you are showing), with 2-3 optima, where one is the global and the other(s) are local. You don't need neural networks or any other ML concept to show this, but only basic calculus (derivatives) and numerical methods (i.e. gradient descent). Just choose a very simple function with more than one optimum and apply the basic gradient descent algorithm. Then you can see that, if you start gradient descent close to one local optimum (i.e. you choose an initial value for $x$ or $\theta$, depending on your notation for the variable of the function) and then you apply gradient descent (for some iterations), you will end up in that close local optimum, from which you cannot escape, after having applied the gradient descent steps.
See also the question Does gradient descent always converge to an optimum? and For convex problems, does gradient in Stochastic Gradient Descent (SGD) always point at the global extreme value?
Well, GD terminates once the gradients are 0, right? Now, in a non-convex function, there could be some points, which do not belong to the global minima, and yet, have 0 gradients. For example, such points can belong to saddle points and local minima.
Consider this picture and say you start GD at the x label.
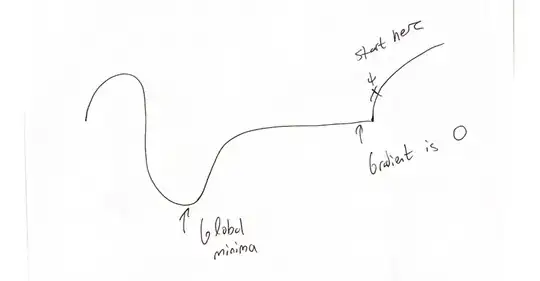
GD will bring you the flat area and will stop making progress there as gradients are 0. However, as you can see, global minima is to the left of this flat region.
By the same token, you have to show, for your own function, that there exists at least a single point whose gradients are 0 and yet, it is not the global minima.
In addition to that, the guarantee on converge for convex functions depends on annealing the learning rate appropriately. For example, if your LR is too high, GD can just keep overshooting the minima. The visualization from this page might help you to understand more regarding the behavior of GD.
There is no way you can be sure you have reached a global minimum. Steepest descent will converge toward where the gradient approaches zero. Depending on the initial conditions ( ie the initial values of the weights) you can and will converge on some minimum. Notice if you run your model several times with random weight initialization you will get slightly different results. What I do find interesting is that it seems that in general the local minima have roughly the same value. The cost function is some kind of surface in N space where N is the number of trainable parameters. We do not know what that surface is like and how many local minimums exist.
