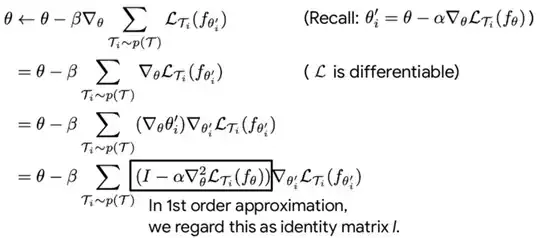Understanding the derivation of the first-order model-agnostic meta-learning

Question

According to the authors of this paper, to improve the performance, they decided to

drop backward pass and using a first-order approximation

I found a blog which discussed how to derive the math but got stuck along the way (please refer to the embedded image below):

1. Why 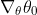disappeared in the next line.
2. How come 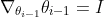(which is an Identity matrix)

Update: I also found another math solution for this. To me it looks less intuitive but there's no confusion with the disappearance of as in the first solution.

Answer 1

$\nabla_{\theta_{i-1}} \theta_{i-1} = \mathbf{I}$ in a similar way that $\frac{d f}{dx} = 1$ for $f(x) = x$. Strictly speaking, $\mathbf{I}$ should be a vector of $1s$ with the same dimensionality as $\theta_{i-1}$, but they are probably abusing notation here and putting such a vector as the diagonal elements of a matrix. Alternatively (actually, the most likely reason!), they are computing the partial derivative of $\theta_{i-1}^j$ with respect to $\theta_{i-1}^k$, for all $k$, for all $j$, which will make up an identity matrix.

Regarding your first question, $\nabla_{\theta} \theta_{0}$ probably becomes 1, but I am not familiar enough with the math of this paper to tell you why. Maybe it's because $\nabla_{\theta} \theta_{0}$ actually means $\nabla_{\theta_0} \theta_{0}$. I would need to dive into it.