What is the benefit of using identity mapping layers in deep neural networks like ResNet?

Question

As I understand, ResNet has some identity mapping layers, whose task is to create the output as the same as the input of the layer. The ResNet solved the problem of accuracy degrading. But what is the benefit of adding identity mapping layers in intermediate layers?

What's the effect of these identity layers on the feature vectors that will be produced in the last layers of the network? Is it helpful for the network to produce better representation for the input? If this expression is correct, what is the reason?

Answer 1

TL;DR: Deep networks have some issues that skip connections fix.

To address this statement:

As I understand Resnet has some identity mapping layers that their task is to create the output as the same as the input of the layer

The residual blocks don't strictly learn the identity mapping. They are simply capable of learning such a mapping. That is, the residual block makes learning the identity function easy. So, at the very least, skip connections will not hurt performance (this is explained formally in the paper).

From the paper:

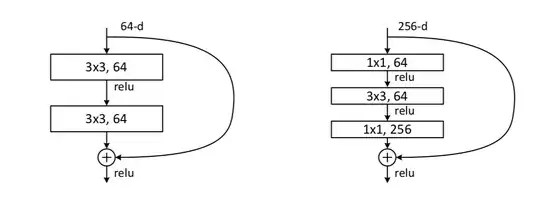
Observe: it's taking some of the layer outputs from earlier layers and passing their outputs further down and element wise summing these with the the outputs from the skipped layers. These blocks may learn mappings that are not the identity map.

From paper (some benefits):

$$\boldsymbol{y} = \mathcal{F}(\boldsymbol{x},\{W_i\})+\boldsymbol{x}\quad\text{(1)}$$The shortcut connections in Eqn.(1) introduce neither extra parameter nor computation complexity. This is not only attractive in practice but also important in our comparisons between plain and residual networks. We can fairly compare plain/residual networks that simultaneously have the same number of parameters, depth, width, and computational cost (except for the negligible element-wise addition).

An example of a residual mapping from the paper is $$\mathcal{F} = W_2\sigma_2(W_1\boldsymbol{x})$$

That is $\{W_i\}$ represents a set of i weight matrices ($W_1,W_2$ in the example) occurring in the layers of the residual (skipped) layers. The "identity shortcuts" are referring to performing the element wise addition of $\boldsymbol{x}$ with the output of the residual layers.

So using the residual mapping from the example (1) becomes:

$$\boldsymbol{y} = W_2\sigma_2(W_1\boldsymbol{x})+\boldsymbol{x}$$

In short, you take the output $\boldsymbol{x}$ of a layer skip it forward and element wise sum it with the output of the residual mapping and thus produce a residual block.

Limitations of deep networks expressed in paper:

When deeper networks are able to start converging, a degradation problem has been exposed: with the network depth increasing, accuracy gets saturated (which might be unsurprising) and then degrades rapidly. Unexpectedly, such degradation is not caused by overfitting, and adding more layers to a suitably deep model leads to higher training error, as reported in [11, 42] and thoroughly verified by our experiments. Fig. 1 shows a typical example.

The skip connections and hence the residual blocks allow for stacking deeper networks while avoiding this degradation issue.

Link to paper

I hope this helps.

Answer 2

As explained in this paper , the major benefit of identity mapping is that it enables backpropagation signal to reach from output (last) layers to input (first) layers.

You can see on the paper at section 2 that it resolves vanishing gradient problem which arises in deeper networks.

Answer 3

As I understand Resnet has some identity mapping layers that their task is to create the output as the same as the input of the layer. the resnet solved the problem of accuracy degrading. But what is the benefit of adding identity mapping layers in intermediate layers?

See this is applicable to deep/very deep networks. We decide to add layers when the model output is not converging to the expected output (it is due to very slow convergence). By this mapping, author has suggested that some portion of complexity of the model can directly be adjusted with input value leaving just residual value for adjustment. The output is mapped to input by identity function - so it is identity mapping. So the shortcut identity mapping is doing the task of some layers in plain neural network.

The identity mapping is applicable only if output and input are of same shape otherwise linear projection is required.

Answer 4

As explained here

only if larger function classes contain the smaller ones are we guaranteed that increasing them strictly increases the expressive power of the network. For deep neural networks, if we can train the newly-added layer into an identity function $f(x)=x$, the new model will be as effective as the original model. As the new model may get a better solution to fit the training dataset, the added layer might make it easier to reduce training errors.