3

To me, most ANN/RNN related articles don't tell me actually how the network is implemented. I know that in the ANN you'll have multiple neurons, activation function, weights, etc. But, how do you, actually, in each neuron, convert the input to the output?

Putting activation function aside, is the neuron simply doing $\text{input}*a+b=\text{output}$, and try to find the correct $a$ and $b$? If it's true, then how about where you have two neurons and their output ($c$ and $d$) is pointing to one neuron? Do you first multiply $c$ and $d$ then feed it in as input?

nbro
  • 42,615
  • 12
  • 119
  • 217
Andrew.Wolphoe
  • 155
  • 6

2 Answers2

4

The basic calculation for a single neuron is of the form

$$\sigma\left(\sum_{i} x_i w_i \right),$$

where $x_i$ is the input to the neuron $w_i$ are the neuron-specific weights for every single input and $\sigma$ is the pre-specified activation function. In your terms, and disregarding the activation function, the calculation would turn out to be

$$c\,a_c + d\,a_d + b$$

Note, that the bias term $b$ is just a weight that gets multiplied by the input $1$, thus it appears to have no input.

If you want to develop a further understanding for this, you should try to get familiar with matrix and vector notations and the basic linear algebra that underlies the feed-forward neural networks. If you do, an entire layer of neurons on a whole batch of data will suddenly simply look like this:

$$\sigma(WX)$$

and a FFNN with say 3 layers will look like this:

$$\sigma_{3}(W_3\sigma_2(W_2\sigma_1(W_1X)))$$

nbro
  • 42,615
  • 12
  • 119
  • 217
Simon Krannig
  • 41
  • 1
2

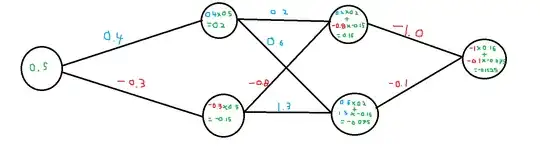
Simon Krannig's answer provides the math notation behined exactly what is going on, but since you still seem a bit confused, I've made a visual representation of a neural network using only weights with no activation function. See below: enter image description here

So I'm fairly sure it as you suspected: At each neuron, you take the sum of the inputs of the previous layer multiplied by the weight that connects that specific input to said neuron, where each input has its own unique weight for every one of its outgoing connections.

With a bias, you would do the exact same math as shown in the above image, but once you find the final value (0.2, -0.15, 0.16 and -0.075, the output layer doesn't have a bias) you would add the bias to the total value. So see below for an example including a bias:

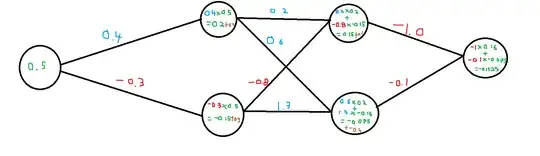
enter image description here

NOTE I did not update the outputs at each layer to include the bias because I can't be bothered redrawing this in paint. Just know that the final value for all the nodes with the brown bias haven't carried over to the next layer.

Then, if you were to include an activation function, you would finally take your value and put it through. So including the bias', looking at node 1 of layer 2, it would be (lets pretend your activation function is a sigmoid):

sigmoid((0.4*0.5)+0.2)

and for layer 3 node 2:

sigmoid(((0.6*0.2)+(1.3*-0.15))-0.4)

That is how you would do a forward pass of a simple neural network.

Recessive
  • 1,446
  • 10
  • 21