I'm implementing a neural network framework from scratch in C++ as a learning exercise. There is one concept I don't see explained anywhere clearly:
How do you go from your last convolutional or pooling layer, which is 3 dimensional, to your first fully connected layer in the network?
Many sources say, that you should flatten the data. Does this mean that you should just simply create a $1D$ vector with a size of $N*M*D$ ($N*M$ is the last convolution layer's size, and $D$ is the number of activation maps in that layer) and put the numbers in it one by one in some arbitrary order?
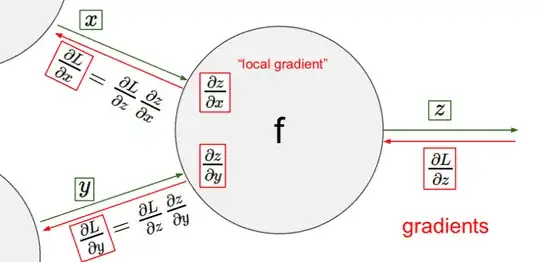
If this is the case, I understand how to propagate further down the line, but how does backprogation work here? Just put the values in reverse order into the activation maps?
I also read that you can do this "flattening" as a tensor contraction. How does that work exactly?