University of Florida/Eml4507/s13.team3.Guzy
< University of Florida < Eml4507
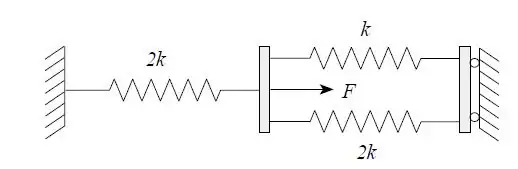
Spring-mass-dashpot system[1] 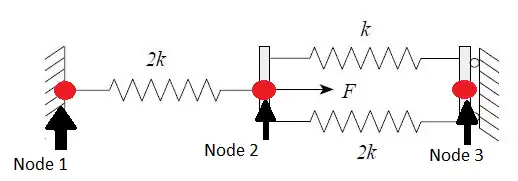
Spring-mass-dashpot system[2]
Problem 2.5: Finite Analysis Of A Spring System

The free body diagram is defined by the matrix
EDU>> Edof=[1 1 2;2 2 3;3 2 3];
Next, create the load force matrix
EDU>> f=[0 100 0];
Next each element stiffness matrix is created
EDU>> K= [0 0 0;0 0 0;0 0 0]; EDU>> k=1500; EDU>> ep1=k; EDU>> ep2=2*k; EDU>> Ke1=springle(ep1); EDU>> Ke2=springle(ep2);
Now we create the global stiffness matrix
EDU>> K=assem(Edof(1,:),K,Ke2); EDU>> K=assem(Edof(2,:),K,Ke1); EDU>> K=assem(Edof(3,:),K,Ke2);
Boundary conditions are now applied
EDU>> bc=[1 0; 3 0]; EDU>> [a,r]=solveq(K,f,bc);
Displacements are found:
EDU>> ed1=extract(Edof(1,:),a)
ed1 =
0 0.0133
EDU>> ed2=extract(Edof(2,:),a)
ed2 =
0.0133 0
EDU>> ed3=extract(Edof(3,:),a)
ed3 =
0.0133 0
Spring forces are evaluated
EDU>> es1=spring1s(ep2,ed1)
es1 =
40
EDU>> es2=spring1s(ep1,ed2)
es2 =
-20
EDU>> es3=spring1s(ep2,ed3)
es3 =
-40
By hand:
- In matrix form: First we create a matrix to show the systems Degree of Freedoms. The first column represents each spring(#1,#2,#3). The second and third column represent the connectivity of each node. The following is a matrix of the Force vector Next we need each element stiffness matrix for every spring: Element stiffness matrix for Spring #1: Element stiffness matrix for Spring #2: Element stiffness matrix for Spring #3: To get the global stiffness matrix, we add up each element stiffness matrix: Plugging each matrix into Hooke's Law we obtain: Because node one and three are attached to the wall, their displacements are zero:
- ↑ http://upload.wikimedia.org/wikiversity/en/b/b1/Fead.s13.sec53a.djvu Obtained from calfem34: p.53-2b]
- ↑ http://upload.wikimedia.org/wikiversity/en/b/b1/Fead.s13.sec53a.djvu Obtained from calfem34: p.53-2b]