Problem Solution
Solution: Taylor series
Error is defined as
![{\displaystyle \displaystyle E_{n}=I-I_{n}=\int _{a}^{b}[f(x)-f_{n}(x)]dx}](../../../a8f279993554a4153164aaf80449ece9dba23669.svg) |
|
For the Taylor series, from the discussion on p6-4, we know that the error is nothing but the remainder of the Taylor series integrated over the given interval i.e
![{\displaystyle \displaystyle \int _{a}^{b}R_{n+1}(x)=\int _{a}^{b}[{\frac {(x-x_{0})^{n+1}}{(n+1)!}}f^{(n+1)}(\xi )]}](../../../8ab6487c73929884f299e58027e21113133f2192.svg) where where ![{\displaystyle \xi \varepsilon [a,b]}](../../../436c63a67c65b658691d7ce6a109ae1b70abc582.svg) |
(1 p2-3) |
For the given function the error is
 |
(2) |
Using the Integral Mean Value Theorem, we have
 |
(3) |
integrating we get,
 |
(4) |
This function has a minimum when  and maximum when
and maximum when  thus we have
thus we have
 |
(5) |
Setting the upper bound of the error to  we have
we have
 |
(6) |
Solving this equation for n we get
 |
(A) |
Solution:Composite Trapezoidal rule
From the discussion on page 16-3 we have
 |
(1) |
where  for
for ![{\displaystyle \zeta \varepsilon [a,b]}](../../../92ebe4f71d2d299091e4c41fff1b7ac95aa98373.svg)
For the given function  , we have
, we have
![{\displaystyle \displaystyle f^{(2)}(x)={\frac {e^{x}[x^{2}-2x+2]-2}{x^{3}}}}](../../../b83c5d6cf9990bca525031b05ce21643f814d584.svg) |
(2) |
Evaluating over the given interval it is seen that the function  has maximum value at
has maximum value at 
![{\displaystyle \displaystyle M_{2}=f^{(2)}(x=1)={\frac {e[1+2-2]-2}{1}}=0.718282}](../../../518ae435d33c67d0effab7c6e49a219f9db986df.svg) |
(3) |
Setting the error to the  and solving for
and solving for  we get
we get
 |
(B) |
Solution :Composite Simpson's Rule
We have from p 17-2, the error estimate of the Composite Simpson's rule as
 |
(1) |
where  for
for ![{\displaystyle \zeta \varepsilon [a,b]}](../../../92ebe4f71d2d299091e4c41fff1b7ac95aa98373.svg)
For the given function  , we have
, we have
![{\displaystyle \displaystyle f^{(4)}(x)={\frac {e^{x}[x^{4}-4x^{3}+12x^{2}-24x]-24}{x^{5}}}}](../../../fc6d886a0976d5d66b2053dd43fac41100edddbf.svg) |
(2) |
Evaluating over the given interval it is seen that the function  has maximum value at
has maximum value at 
![{\displaystyle \displaystyle M_{4}=f^{(4)}(x=1)={\frac {e[1-4+12-24+24]-24}{1}}=9(e)-24=0.464536}](../../../6a3bcf3c09ea3d5e20cf690592c2be2bdd0d637a.svg) |
(3) |
Setting the error to the  and solving for
and solving for  we get
we get
 |
(c) |
Part 2:Numerical determination of power of h
In order to verify the power of  in the error, data from Problem 8 of HW1 is used.
in the error, data from Problem 8 of HW1 is used.
In the case of a Semilog plot (log(y) vs x), an equation of the form

such that

From the above equation it is seen that if the plot on a semilog graph is a straight line then the relationship between the two variables is exponential.
A log-log plot(log(y) vs log(x)) is a similar plot, for which the equation is of the form
![{\displaystyle {\boldsymbol {log(Y)=a[log(X)]+b}}}](../../../9e6add704d58cc2a0459b3f847699db9b950d6eb.svg)
such that, 
This discussion is used in the interpretation of the graphs given below.
It is readily seen that the slope of the line in the log-log graph is the power of the x variable.
Composite trapezoidal Rule
Given below is the data from the numerical evaluation of the given function using Composite Trapezoidal Rule.
Composite Trapezoidal Rule |
No. of terms  |
Absolute Error  |

|
2 |
1.3282917278 |
0.5 |
4 |
1.3205046195 |
0.25 |
8 |
1.3185530869 |
0.125 |
16 |
1.3180649052 |
0.0625 |
32 |
1.3179428411 |
0.03125 |
64 |
1.3179123240 |
0.015625 |
128 |
1.3179046946 |
0.0078125 |
256 |
1.3179027872 |
0.00390625 |
512 |
1.3179023104 |
0.001953125 |
1024 |
1.3179021912 |
0.000976563 |
First we plot a semilog graph for the data. The graph is shown below:
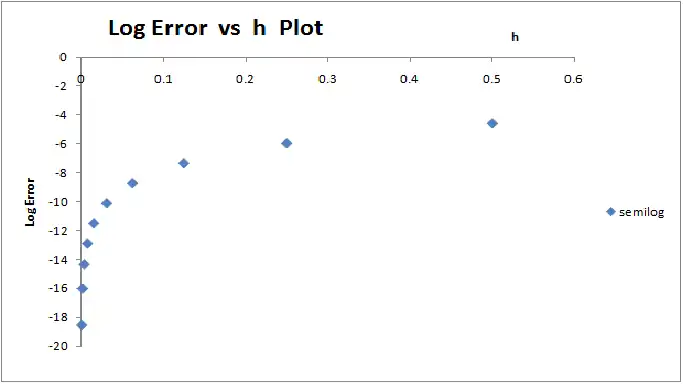
The graph is not a straight line which implies that the relationship between  and
and  is not exponential. Hence we plot a log-log graph as below:
is not exponential. Hence we plot a log-log graph as below:
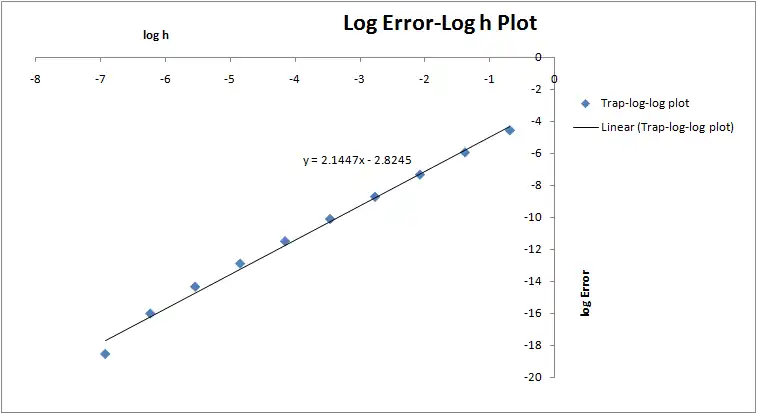
This is seen to be linear. A straight line if fitted to the data the equation of which is given above. From the discussion above, we see that the slope of line is 2.1447 which is very close to the analytical value of 2.
Composite Simpson's Rule
Given below is the data obtained from HW1 for the COmposite Simpsons Rule.
Composite Simpson's Rule |
No. of terms  |
Absolute Error  |

|
2 |
1.318008666 |
0.5 |
4 |
1.317908917 |
0.25 |
8 |
1.317902576 |
0.125 |
16 |
1.317902178 |
0.0625 |
Plotting a semilog graph of  against
against  we see that it is non-linear as in the case of the Composite Trapezoidal Rule.
we see that it is non-linear as in the case of the Composite Trapezoidal Rule.
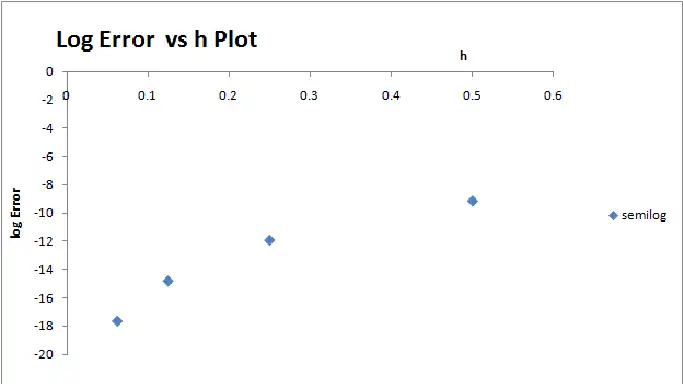
Thus, plotting the log-log graph as below,
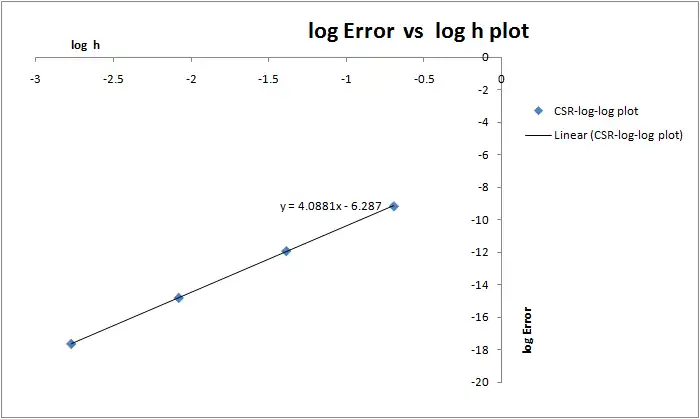
we see that the slope of the line is 4.0881 which is very close to the analytically determined value of 4.
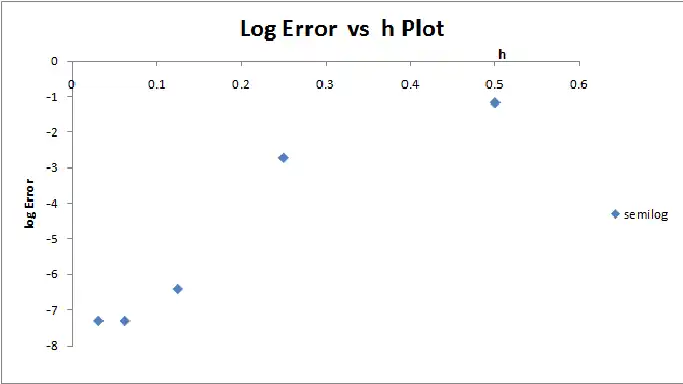
Taylor Series
Given below is the data for the Taylor series method. Eventhough  is not used in the Taylor series method,defining
is not used in the Taylor series method,defining  based on the number of terms of the series, it is seen that the error and h are not related exponentially or by a power relation i.e. both semilog and log log plots are not linear.
based on the number of terms of the series, it is seen that the error and h are not related exponentially or by a power relation i.e. both semilog and log log plots are not linear.
Taylor Series |
No. of terms  |
Absolute Error  |

|
2 |
1.2500000 |
0.5 |
4 |
1.3159722222 |
0.25 |
8 |
1.3179018152 |
0.125 |
16 |
1.3179021515 |
0.0625 |
32 |
1.3179021515 |
0.03125 |
--Egm6341.s10.team2.niki 08:10, 17 February 2010 (UTC)




