R5.6
solved by Luca Imponenti
Problem Statement
Complete the solution to the following problem

where
![{\displaystyle y_{h}=e^{-2x}[Acos(3x)+Bsin(3x)]\!}](../../../792e67f127ff688d55ed48d9f0303345b9a28184.svg)
and
![{\displaystyle y_{p}=xe^{-2x}[Mcos(3x)+Nsin(3x)]\!}](../../../96a697d5683642f371e1127b4a15314d1a2b93f0.svg)
Find the overall solution  corresponds to the initial condition:
corresponds to the initial condition:

- Plot the solution over 3 periods.
Taking the derivatives of the particular solution 
Particular Solution
![{\displaystyle y_{p}=xe^{-2x}[Mcos(3x)+Nsin(3x)]\!}](../../../96a697d5683642f371e1127b4a15314d1a2b93f0.svg)
![{\displaystyle y'_{p}=e^{-2x}[sin(3x)(N-2Nx-3Mx)+cos(3x)(3Nx+M-2Mx)]\!}](../../../4229480759610de8da772b0745c06b16b70b56ae.svg)
![{\displaystyle y''_{p}=e^{-2x}[sin(3x)(12Mx-6M-5Nx-4N)+cos(3x)(6N-5Mx-4M-12Nx)]\!}](../../../57b163ea521277f918af0d523c1e8f0ca8e234ff.svg)
Plugging these into the ODE yields

![{\displaystyle 4[sin(3x)(N-2Nx-3Mx)+cos(3x)(3Nx+M-2Mx)]+}](../../../2edffedd7a2b90e82102acd19a704b0b273dc2fd.svg)
![{\displaystyle 13x[Mcos(3x)+Nsin(3x)]=2cos(3x)\!}](../../../d9655d1493f66fa3a0f7589a9c3631d9b4476def.svg)
Equating like terms allows us to solve for M and N
![{\displaystyle sin(3x)[(12Mx-6M-5Nx-4N)+4(N-2Nx-3Mx)+13Nx]=0\!}](../../../a020f3dd194ee3d5cfeabb37b2da5e9f270c8290.svg)
![{\displaystyle cos(3x)[(6N-5Mx-4M-12Nx)+4(3Nx+M-2Mx)+13Mx]=2cos(3x)\!}](../../../61f7febe8c0331fa45a5d99aafb6b7551136061a.svg)



So the particular solution is

Overall Solution
The overall solution in the sum of the homogeneous and particular solutions

![{\displaystyle y(x)=e^{-2x}[Acos(3x)+Bsin(3x)]+{\frac {1}{3}}xe^{-2x}sin(3x)\!}](../../../b9ba4455133d526b6750b7d4ad088a2b3ebeb60a.svg)
To find A and B we apply the initial conditions


Taking the derivative
![{\displaystyle y'(x)={\frac {d}{dx}}[e^{-2x}[cos(3x)+Bsin(3x)]+{\frac {1}{3}}xe^{-2x}sin(3x)]\!}](../../../8363fdca8c2a01fd5519870363c110a30f746261.svg)
![{\displaystyle y'(x)=e^{-2x}[(3B+x-2)cos(3x)-(2B+{\frac {2}{3}}x+{\frac {8}{3}})sin(3x)]\!}](../../../c86f7dc58a6220ae49af31a9fe4e261acfa83019.svg)


Giving us the overall solution
![{\displaystyle y(x)=e^{-2x}[cos(3x)+{\frac {2}{3}}sin(3x)+{\frac {1}{3}}xsin(3x)]\!}](../../../c0df58d196d9072113ac3bbd23846cbeaa804059.svg)
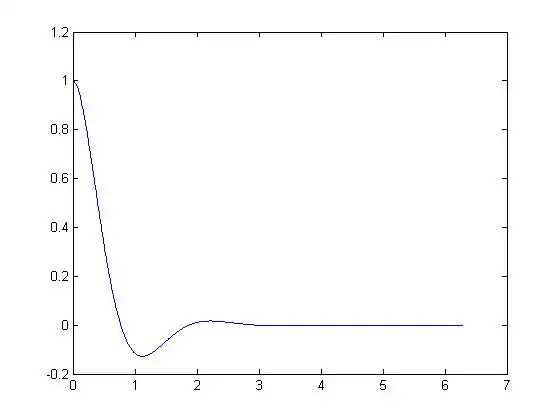
Plot
The period for  is
is 
Plotting the solution  over 3 periods yields
over 3 periods yields
Egm4313.s12.team11.imponenti (talk) 01:56, 30 March 2012 (UTC)
