Part 3
Solved by Luca Imponenti
Find  , for
, for  such that:
such that:

for  in
in ![{\displaystyle [0.9,3]\!}](../../../bb2c515c8c74080e5a7916ac7bd889dc9164916e.svg) with the initial conditions found.
with the initial conditions found.
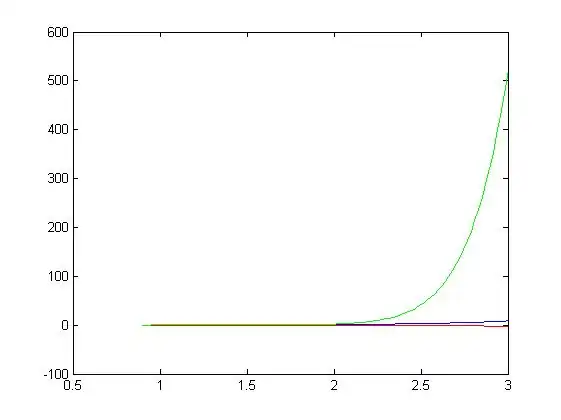
Plot  for
for  for
for  in
in ![{\displaystyle [0.9,3]\!}](../../../bb2c515c8c74080e5a7916ac7bd889dc9164916e.svg) .
.
Homogeneous Solution
The homogeneous case is shown below:

This equation has the following roots:

Which gives yields the homogeneous solution

General Solution, n=4
Using the taylor series approximation from earlier with  we have
we have

We know the particular solution,  , ve will have this form:
, ve will have this form:

taking the derivatives of this solution

and

Plugging the above equations into the original ODE yields the following matrix equation:

The unknown vector  can be easily solved by forward substitution,the following values were calculated in matlab:
can be easily solved by forward substitution,the following values were calculated in matlab:

So the particular solution  is
is

We can now find the general solution for n=4,  .
.



Solving using the initial conditions yields;


General Solution, n=7
Using the taylor series approximation from earlier with  we have
we have

In a similar fashion we construct a matrix equation for n=7:

Solving:

So the particular solution  is
is

We can now find the general solution for n=7,  .
.



Solving using our initial conditions yields



General Solution, n=11
Using the taylor series approximation from earlier with  we have
we have


Finally, we write out the matrix equation for n=11:


Solving the system in matlab:


So the particular solution  is
is


We can now find the general solution for n=11,  .
.




Solving using our initial conditions yields




Plot
 shown in red
shown in red
 shown in blue
shown in blue
 shown in green
shown in green