University of Florida/Egm4313/s12.team11.imponenti/R3.1

Report 3, Problem 1

Problem Statement

Find the solution to the following L2-ODE-CC: $y''-10y'+25y=r(x)\!$

With the following excitation: $r(x)=7e^{5x}-2x^{2}\!$

And the following initial conditions: $y(0)=4,y'(0)=-5\!$

Plot this solution and the solution in the example on p.7-3

Homogeneous Solution

To find the homogeneous solution we need to find the roots of our equation

$\lambda ^{2}-10\lambda +25=0\!$ $(\lambda -5)(\lambda -5)=0\!$ $\lambda =5\!$

We know the homogeneous solution for the case of a real double root with $\lambda =5\!$ to be

$y_{h}=c_{1}e^{5x}+c_{2}xe^{5x}\!$

Particular Solution

For the given excitation we must use the Sum Rule to the particular solution as follows

$y_{p}=y_{p1}+y_{p2}\!$ where $y_{p1}\!$ and $y_{p2}\!$ are the solutions to $r_{1}(x)=7e^{5x}\!$ and $r_{2}(x)=-2x^{2}\!$ , respectively

First Particular Solution

$r_{1}(x)=7e^{5x}\!$ ,

from table 2.1, K 2011, pg. 82 we have

$y_{p1}=Ce^{5x}\!$

but this corresponds to one of our homogeneous solutions so we must use the modification rule to get

$y_{p1}=Cx^{2}e^{5x}\!$

Plugging this into the original L2-ODE-CC then substituting;

$y_{p1}''-10y_{p1}'+25y_{p1}=r_{1}(x)\!$

$(Cx^{2}e^{5x})''-10(Cx^{2}e^{5x})'+25(Cx^{2}e^{5x})=r_{1}(x)\!$

$25Cx^{2}e^{5x}+10Cxe^{5x}+10Cxe^{5x}+2Ce^{5x}-10(5Cx^{2}e^{5x}+2Cxe^{5x})+25Cx^{2}e^{5x}=7e^{5x}\!$

$e^{5x}[25Cx^{2}+10Cx+10Cx+2C-50Cx^{2}-20Cx+25Cx^{2}]=7e^{5x}\!$

$e^{5x}2C=7e^{5x}\!$

so $C={\frac {7}{2}}\!$ and the first particular solution is,

y_{p1}={\frac {7}{2}}x^{2}e^{5x}\!

Second Particular Solution

$r_{2}(x)=-2x^{2}\!$ ,

from table 2.1, K 2011, pg. 82 we have

$y_{p2}=a_{2}x^{2}+a_{1}x+a_{0}\!$

Plugging this into the original L2-ODE-CC then substituting;

$y_{p2}''-10y_{p2}'+25y_{p2}=r_{2}(x)\!$

$(a_{2}x^{2}+a_{1}x+a_{0})''-10(a_{2}x^{2}+a_{1}x+a_{0})'+25(a_{2}x^{2}+a_{1}x+a_{0})=-2x^{2}\!$

$2a_{2}-10(2a_{2}x+a_{1})+25(a_{2}x^{2}+a_{1}x+a_{0})=-2x^{2}\!$

grouping like terms we get three equations to solve for the three unknowns, these are written in matrix form

$25a_{2}x^{2}+(25a_{1}-20a_{2})x+(25a_{0}-10a_{1}+2a_{2})=-2x^{2}\!$

{\begin{bmatrix}2&-10&25\\-20&25&0\\25&0&0\end{bmatrix}}{\begin{bmatrix}a_{2}\\a_{1}\\a_{0}\end{bmatrix}}={\begin{bmatrix}0\\0\\-2\end{bmatrix}}\!

solving by back subsitution leads to $a_{2}=-{\frac {2}{25}},a_{1}={\frac {8}{125}},a_{0}={\frac {4}{125}}\!$

so the second particular solution is,

y_{p2}=-{\frac {2}{25}}x^{2}+{\frac {8}{125}}x+{\frac {4}{125}}\!

General Solution

The general solution is the summation of the homogeneous and particular solutions

$y=y_{h}+y_{p1}+y_{p2}\!$

$y=c_{1}e^{5x}+c_{2}xe^{5x}+{\frac {7}{2}}x^{2}e^{5x}-{\frac {2}{25}}x^{2}+{\frac {8}{125}}x+{\frac {4}{125}}\!$

$y=e^{5x}(c_{1}+c_{2}x+{\frac {7}{2}}x^{2})-{\frac {2}{25}}x^{2}+{\frac {8}{125}}x+{\frac {4}{125}}\!$

Applying the first initial condition $y(0)=4\!$

$y(0)=c_{1}+{\frac {4}{125}}=4\!$

$c_{1}={\frac {496}{125}}\!$

Second initial condition $y'(0)=-5\!$

$y'={\frac {d}{dx}}y=e^{5x}[5(c_{1}+c_{2}x+{\frac {7}{2}}x^{2})+c_{2}+7x]-{\frac {4}{25}}x+{\frac {8}{125}}\!$

$y'=e^{5x}[{\frac {35}{2}}x^{2}+(5c_{2}+7)x+5c_{1}+c_{2}]-{\frac {4}{25}}x+{\frac {8}{125}}\!$

$y'(0)=5c_{1}+c_{2}+{\frac {8}{125}}=-5\!$

$c_{2}=-{\frac {3113}{125}}\!$

The general solution to the differential equation is therefore

                     $y(x)=e^{5x}({\frac {496}{125}}-{\frac {3113}{125}}x+{\frac {7}{2}}x^{2})-{\frac {2}{25}}x^{2}+{\frac {8}{125}}x+{\frac {4}{125}}\!$

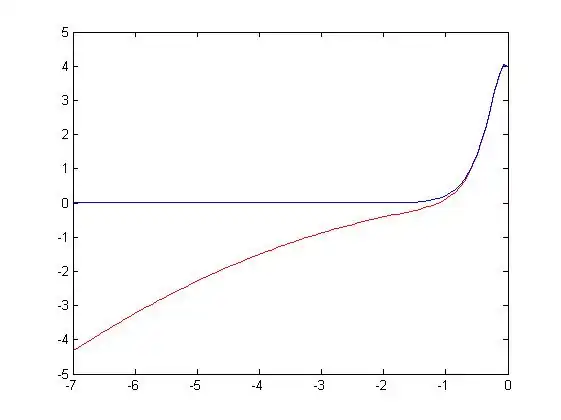
Plot

Below is a plot of this solution and the solution to in the example on p.7-3

our solution $y(x)=e^{5x}({\frac {496}{125}}-{\frac {3113}{125}}x+{\frac {7}{2}}x^{2})-{\frac {2}{25}}x^{2}+{\frac {8}{125}}x+{\frac {4}{125}}\!$ (shown in red)

example on p.7-3 $y(x)=e^{5x}(4-25*x+*{\frac {7}{2}}x^{2})\!$ (shown in blue)

Egm4313.s12.team11.imponenti 22:31, 20 February 2012 (UTC)