Report 2, Problem 9
Problem Statement
Find and plot the solution for the L2-ODE-CC corresponding to

with 
and initial conditions  ,
, 
In another figure, superimpose 3 figs.:(a)this fig. (b) the fig. in R2.6 p.5-6, and (c) the fig. in R2.1 p.3-7
Quadratic Equation
 with
with 


Homogeneous Solution
The solution to a L2-ODE-CC with two complex roots is given by
![{\displaystyle y(x)=e^{-{\frac {a}{2}}x}[Acos(\omega x)+Bsin(\omega x)]\!}](../../../510ae7db6943e388e2cd367f1aa44fc4f13f8348.svg)
where 
![{\displaystyle y(x)=e^{-2x}[Acos(3x)+Bsin(3x)]\!}](../../../6d7f71b17955c0f76363ac0f6b573e69e0eb226c.svg)
Solving for A and B
first initial condition 
![{\displaystyle y(x)=e^{-2x}[Acos(3x)+Bsin(3x)]\!}](../../../6d7f71b17955c0f76363ac0f6b573e69e0eb226c.svg)
![{\displaystyle y(0)=e^{-2*0}[Acos(3*0)+Bsin(3*0)]=1\!}](../../../a61630cc21c2412df2d9bfbe52a1f738cd572f1a.svg)

second initial condition 
![{\displaystyle y'(x)={\frac {d}{dx}}y(x)={\frac {d}{dx}}e^{-2x}[cos(3x)+Bsin(3x)]\!}](../../../cbb043b16f50f0ecab2705db00e771bca7457aba.svg)
![{\displaystyle y'(x)=e^{-2x}[(-2B-3)sin(3x)+(3B-2)cos(3x)]\!}](../../../30434049e26751b730283ee9687ba5ea0a8e815c.svg)
![{\displaystyle y'(0)=e^{-2*0}[(-2B-3)sin(3*0)+(3B-2)cos(3*0)]\!}](../../../be62daa0beda99ce3a4804d3ccce9faedbef87f6.svg)


so the solution to our L2-ODE-CC is
![{\displaystyle y(x)=e^{-2x}[cos(3x)+{\frac {2}{3}}sin(3x)]\!}](../../../7bbd97a09c6c3f88feb037232191230bd797f00d.svg)
Solution to R2.6
After solving for the constants  and
and  we have the following homogeneous equation
we have the following homogeneous equation

Characteristic Equation and Roots


We have a real double root 
Homogeneous Solution
We know the homogeneous solution to a L2-ODE-CC with a double real root to be

Assuming object starts from rest
 ,
, 
Plugging in  and applying our first initial condition
and applying our first initial condition


Taking the derivative and applying our second condition




Giving us the final solution

Plots
Solution to this Equation
![{\displaystyle y(x)=e^{-2x}[cos(3x)+{\frac {2}{3}}sin(3x)]\!}](../../../7bbd97a09c6c3f88feb037232191230bd797f00d.svg)

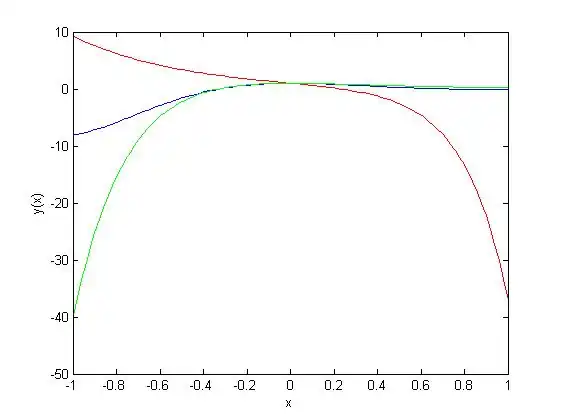
Superimposed Graph
Our solution: ![{\displaystyle y(x)=e^{-2x}[cos(3x)+{\frac {2}{3}}sin(3x)]\!}](../../../7bbd97a09c6c3f88feb037232191230bd797f00d.svg) shown in blue
shown in blue
Equation for fig. in R2.1 p.3-7:  shown in red
shown in red
Equation for fig. in R2.6 p.5-6: shown in green
shown in green
Egm4313.s12.team11.imponenti 03:38, 8 February 2012 (UTC)

