University of Florida/Egm4313/s12.team11.R5

Given: Find ${\displaystyle R_{c}\!}$ for the following series:

1. ${\displaystyle r(x)=\sum _{k=0}^{\infty }(k+1)kx^{k}\!}$
2. ${\displaystyle r(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{\gamma ^{k}}}x^{2k}\!}$

Find ${\displaystyle R_{c}\!}$ for the Taylor series of

3. ${\displaystyle sin(x)\!}$ at ${\displaystyle x=0\!}$

4. ${\displaystyle log(1+x)\!}$ at ${\displaystyle x=0\!}$

5. ${\displaystyle log(1+x)\!}$ at ${\displaystyle x=1\!}$

The radius of convergence ${\displaystyle R_{c}\!}$ is defined as

${\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {d_{k+1}}{d_{k}}}|]^{-1}\!}$

1. ${\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {(k+2)(k+1)}{(k+1)(k)}}|]^{-1}\!}$
${\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {(k+2)}{(k)}}|]^{-1}\!}$
${\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {k(1+{\frac {2}{k}})}{k}}|]^{-1}\!}$
${\displaystyle R_{c}=[\lim _{k\to \infty }|1+{\frac {2}{k}}|]^{-1}\!}$
${\displaystyle R_{c}=[1+0]^{-1}\!}$

                                                          ${\displaystyle R_{c}=1\!}$

2. ${\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {\frac {(-1)^{k+1}}{\gamma ^{k+1}}}{\frac {(-1)^{k}}{\gamma ^{k}}}}|]^{-1}\!}$
${\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {-1}{\gamma }}|]^{-1}\!}$
${\displaystyle R_{c}=[\lim _{k\to \infty }{\frac {1}{\gamma }}]^{-1}\!}$
${\displaystyle R_{c}=[{\frac {1}{\gamma }}]^{-1}\!}$
${\displaystyle R_{c}=\gamma \!}$

However, in this problem, the series ${\displaystyle x\!}$ term is ${\displaystyle x^{2k}\!}$ not ${\displaystyle x^{k}\!}$, as is the general form.
Therefore, this implies:

${\displaystyle |x^{2}|=\gamma \!}$
${\displaystyle |x|={\sqrt {\gamma }}\!}$

                                                        ${\displaystyle R_{c}={\sqrt {\gamma }}\!}$

3. The Taylor series for ${\displaystyle sin(x)\!}$ is expressed as ${\displaystyle sin(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}\!}$

${\displaystyle \lim _{k\to \infty }{\frac {{\frac {(-1)^{k+1}}{(2(k+1)+1)!}}x^{2(k+1)+1}}{{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}}}\!}$

${\displaystyle \lim _{k\to \infty }{\frac {{\frac {1}{(2k+3)!}}x^{2k+3}}{{\frac {1}{(2k+1)!}}x^{2k+1}}}\!}$

${\displaystyle \lim _{k\to \infty }{\frac {{\frac {1}{(2k+3)}}x^{3}}{x}}\!}$

${\displaystyle \lim _{k\to \infty }{\frac {1}{(2k+3)}}x^{2}\!}$

Therefore: ${\displaystyle R_{c}=[\lim _{k\to \infty }{\frac {1}{(2k+3)}}]^{-1}\!}$

                                                           ${\displaystyle R_{c}=\infty \!}$

4. The Taylor series for ${\displaystyle log(1+x)\!}$ at ${\displaystyle x=0\!}$ is expressed as ${\displaystyle log(1+x)=\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}}{k}}x^{k}\!}$

${\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {\frac {(-1)^{k+2}}{k+1}}{\frac {(-1)^{k+1}}{k}}}|]^{-1}\!}$

${\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {\frac {(-1)}{k+1}}{\frac {(1)}{k}}}|]^{-1}\!}$

${\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {\frac {(-1)}{k(1+{\frac {1}{k}})}}{\frac {1}{k}}}|]^{-1}\!}$

${\displaystyle R_{c}=[\lim _{k\to \infty }|{\frac {(-1)}{(1+{\frac {1}{k}})}}|]^{-1}\!}$

${\displaystyle R_{c}=[1/1]^{-1}\!}$

                                                             ${\displaystyle R_{c}=1\!}$

5. The Taylor series for ${\displaystyle log(1+x)\!}$ at ${\displaystyle x=1\!}$ is expressed as ${\displaystyle log(1+x)=log(2)+\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}}{2^{k}k}}(x-1)^{k}\!}$

${\displaystyle \lim _{k\to \infty }{\frac {{\frac {(-1)^{k+2}}{2^{k+1}(k+1)}}(x-1)^{k+1}}{{\frac {(-1)^{k+1}}{2^{k}k}}(x-1)^{k}}}\!}$

${\displaystyle \lim _{k\to \infty }{\frac {{\frac {(-1)^{2}}{2(k+1)}}(x-1)}{\frac {1}{k}}}\!}$

${\displaystyle \lim _{k\to \infty }{\frac {{\frac {1}{2k(1+{\frac {1}{k}})}}(x-1)}{\frac {1}{k}}}\!}$

${\displaystyle \lim _{k\to \infty }{\frac {{\frac {1}{2(1+{\frac {1}{k}})}}(x-1)}{1}}\!}$

${\displaystyle {\frac {1}{2}}(x-1)\!}$

For convergence: ${\displaystyle {\frac {1}{2}}(x-1)<1\!}$

${\displaystyle x-1<2\!}$

${\displaystyle x<3\!}$

Therefore,

                                                             ${\displaystyle R_{c}=3\!}$

Part 1:Determine whether the following are linearly independent using the Wronskian

Part 2: Determine whether the following are linearly independent using the Gramian

By both methods (the Wronskian and the Gramian) we obtain the same results.

Verify using the Gramian that the following two vectors are linearly independent.

${\displaystyle \mathbf {b_{1}} =2\mathbf {e_{1}} +7\mathbf {e_{2}} \!}$
${\displaystyle \mathbf {b_{1}} =1.5\mathbf {e_{1}} +3\mathbf {e_{2}} \!}$

${\displaystyle \Gamma (f,g)=det{\begin{bmatrix}\langle \mathbf {b1} ,\mathbf {b1} \rangle &\langle \mathbf {b1} ,\mathbf {b2} \rangle \\\langle \mathbf {b2} ,\mathbf {b1} \rangle &\langle \mathbf {b2} ,\mathbf {b2} \rangle \end{bmatrix}}\!}$

We know from (3) 8-9 that:
${\displaystyle \langle \mathbf {b1} ,\mathbf {b2} \rangle =\mathbf {b1} \cdot \mathbf {b2} <br>\!}$

We obtain,
${\displaystyle \langle \mathbf {b1} ,\mathbf {b1} \rangle =(2)(2)+(7)(7)=4+49=53\!}$
${\displaystyle \langle \mathbf {b1} ,\mathbf {b2} \rangle =\langle \mathbf {b2} ,\mathbf {b1} \rangle =(1.5)(2)+(7)(3)=3+21=24\!}$ ${\displaystyle \langle \mathbf {b2} ,\mathbf {b2} \rangle =(1.5)(1.5)+(3)(3)=2.25+9=11.25\!}$

Then,
${\displaystyle \Gamma (f,g)=det{\begin{bmatrix}53&24\\24&11.25\end{bmatrix}}=596.25-576=20.25\neq 0\!}$

                                           ${\displaystyle \therefore \!}$ b_1 and b_2 are linearly independent

Show that ${\displaystyle y_{p}(x)=\sum _{i=0}^{n}y_{p,i}(x)\!}$ is indeed the overall particular solution of the L2-ODE-VC ${\displaystyle y''+p(x)y'+q(x)y=r(x)\!}$ with the excitation ${\displaystyle r(x)=r_{1}(x)+r_{2}(x)+...+r_{n}(x)=\sum _{i=0}^{n}r_{i}(x)\!}$.

Discuss the choice of ${\displaystyle y_{p}(x)\!}$ in the above table e.g., for ${\displaystyle r(x)=k\cos \omega x\!}$ why would you need to have both ${\displaystyle \cos \omega x\!}$ and ${\displaystyle \sin \omega x\!}$ in ${\displaystyle y_{p}(x)\!}$ ?

Because the ODE is a linear equation in y and its derivatives with respect to x, the superposition principle can be applied:

${\displaystyle r_{1}(x)\!}$ is a specific excitation with known form of ${\displaystyle y_{p1}(x)\!}$ and ${\displaystyle r_{2}(x)\!}$ is a specific excitation with known form of ${\displaystyle y_{p2}(x)\!}$

${\displaystyle +{\begin{cases}&{\text{ }}y_{p1}''+p(x)y_{p1}'+q(x)y_{p1}=r_{1}(x)\\&{\text{ }}y_{p2}''+p(x)y_{p2}'+q(x)y_{p2}=r_{2}(x)\end{cases}}\!}$

becomes

${\displaystyle (y_{p1}+y_{p2})''+p(x)(y_{p1}+y_{p2})'+q(x)(y_{p1}+y_{p2})=r_{1}(x)+r_{2}(x)\!}$

proving that

${\displaystyle y_{p}(x)=\sum _{i=0}^{n}y_{p,i}(x)\!}$ is indeed the overall particular solution of the L2-ODE-VC ${\displaystyle y''+p(x)y'+q(x)y=r(x)\!}$ with the excitation ${\displaystyle r(x)=\sum _{i=0}^{n}r_{i}(x)\!}$

According to Fourier Theorem periodic functions can be represented as infinite series in terms of cosines and sines:

${\displaystyle f(x)=a_{0}+\sum _{n=1}^{\infty }[a_{n}\cos \omega x+b_{n}\sin \omega x]\!}$

where the coefficients ${\displaystyle a_{0},a_{n},b_{n}\!}$ are the Fourier coefficients calculated using Euler formulas.

So even though the system is being excited by functions like ${\displaystyle r(x)=k\cos \omega x\!}$ the particular solution would still include both ${\displaystyle \sin \omega x\!}$ and ${\displaystyle \cos \omega x\!}$ in ${\displaystyle y_{p}(x)\!}$ because the excitation is a periodic function that can be represented as the Fourier infinite series in terms of both ${\displaystyle \sin \omega x\!}$ and ${\displaystyle \cos \omega x\!}$ times the Fourier coefficients

Complete the solution to the following problem

${\displaystyle y''+4y'+13y=2e^{-2x}cos(3x)\!}$

where

${\displaystyle y_{h}=e^{-2x}[Acos(3x)+Bsin(3x)]\!}$

and

${\displaystyle y_{p}=xe^{-2x}[Mcos(3x)+Nsin(3x)]\!}$

Find the overall solution ${\displaystyle y(x)\!}$ corresponds to the initial condition:

${\displaystyle y(0)=1\ ,\ y'(0)=0\!}$

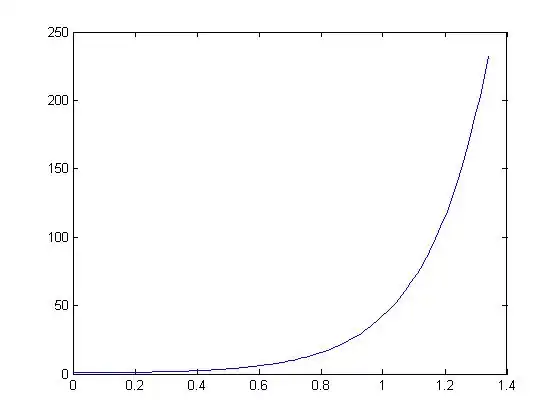
Plot the solution over 3 periods.

Taking the derivatives of the particular solution ${\displaystyle y_{p}(x)\!}$

${\displaystyle y_{p}=xe^{-2x}[Mcos(3x)+Nsin(3x)]\!}$

${\displaystyle y'_{p}=e^{-2x}[sin(3x)(N-2Nx-3Mx)+cos(3x)(3Nx+M-2Mx)]\!}$

${\displaystyle y''_{p}=e^{-2x}[sin(3x)(12Mx-6M-5Nx-4N)+cos(3x)(6N-5Mx-4M-12Nx)]\!}$

Plugging these into the ODE yields

${\displaystyle sin(3x)(6M-12Mx+5Nx+4N)+cos(3x)(5Mx+4M+12Nx-6N)+\!}$ ${\displaystyle 4[sin(3x)(N-2Nx-3Mx)+cos(3x)(3Nx+M-2Mx)]+}$ ${\displaystyle 13x[Mcos(3x)+Nsin(3x)]=2cos(3x)\!}$

Equating like terms allows us to solve for M and N

${\displaystyle sin(3x)[(12Mx-6M-5Nx-4N)+4(N-2Nx-3Mx)+13Nx]=0\!}$

${\displaystyle cos(3x)[(6N-5Mx-4M-12Nx)+4(3Nx+M-2Mx)+13Mx]=2cos(3x)\!}$

${\displaystyle -6M=0\!}$

${\displaystyle 6N=2\!}$

${\displaystyle M=0\ ,\ N={\frac {1}{3}}\!}$

So the particular solution is

${\displaystyle y_{p}={\frac {1}{3}}xe^{-2x}sin(3x)\!}$

The overall solution in the sum of the homogeneous and particular solutions

${\displaystyle y(x)=y_{h}(x)+y_{p}(x)\!}$

${\displaystyle y(x)=e^{-2x}[Acos(3x)+Bsin(3x)]+{\frac {1}{3}}xe^{-2x}sin(3x)\!}$

To find A and B we apply the initial conditions

${\displaystyle y(0)=1\ ,\ y'(0)=0\!}$

${\displaystyle y(0)=1=A\!}$

Taking the derivative

${\displaystyle y'(x)={\frac {d}{dx}}[e^{-2x}[cos(3x)+Bsin(3x)]+{\frac {1}{3}}xe^{-2x}sin(3x)]\!}$

${\displaystyle y'(x)=e^{-2x}[(3B+x-2)cos(3x)-(2B+{\frac {2}{3}}x+{\frac {8}{3}})sin(3x)]\!}$

${\displaystyle y'(0)=0=3B-2\!}$

${\displaystyle B={\frac {2}{3}}\!}$

Giving us the overall solution

   ${\displaystyle y(x)=e^{-2x}[cos(3x)+{\frac {2}{3}}sin(3x)+{\frac {1}{3}}xsin(3x)]\!}$

The period for ${\displaystyle cos(3x)\ ,\ sin(3x)\!}$ is ${\displaystyle {\frac {2\pi }{3}}}$

Plotting the solution ${\displaystyle y(x)\!}$ over 3 periods yields

${\displaystyle v=4e_{1}+2e_{2}=c_{1}b_{1}+c{2}b_{2}\!}$

${\displaystyle b_{1}=2e_{1}+7e_{2}\!}$

${\displaystyle b_{2}=1.5e_{1}+3e_{2}\!}$

1. Find the components ${\displaystyle c_{1},c_{2}\!}$ using the Gram matrix.
2. Verify the result by using ${\displaystyle b_{1}\!}$ and ${\displaystyle b_{2}\!}$, and rely on the non-zero determinant matrix of ${\displaystyle b_{1}\!}$ and ${\displaystyle b_{2}\!}$ relative to the bases of ${\displaystyle e_{1}\!}$ and ${\displaystyle e_{2}\!}$.

${\displaystyle v=4e_{1}+2e_{2}\equiv c_{1}b_{1}+c_{2}b_{2}\!}$

${\displaystyle c_{1}b_{1}+c_{2}b_{2}=(-2)(2e_{1}+7e_{2})+(5.33)(1.5e_{1}+3e_{2})\!}$

${\displaystyle c_{1}b_{1}+c_{2}b_{2}=-4e_{1}-14e_{2}+8e_{1}+16e_{2}\!}$

${\displaystyle c_{1}b_{1}+c_{2}b_{2}=4e_{1}+2e_{2}\!}$

${\displaystyle v=4e_{1}+2e_{2}\equiv c_{1}b_{1}+c_{2}b_{2}\!}$

                                                     ${\displaystyle \therefore \!}$ solution is correct

Find the integral

${\displaystyle \int x^{n}log(1+x)dx\!}$ for ${\displaystyle n=0\!}$ and ${\displaystyle n=1\!}$

Using integration by parts, and then with the help of of

General Binomial Theorem

${\displaystyle (x+y)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}x^{n-k}y^{k}\!}$

For ${\displaystyle n=0\!}$:

${\displaystyle \int x^{0}log(1+x)dx=\int log(1+x)dx\!}$

For substitution by parts, ${\displaystyle u=log(1+x),du={\frac {1}{1+x}},dv=dx,v=x\!}$

${\displaystyle \int log(1+x)dx=xlog(1+x)-\int {\frac {x}{1+x}}dx\!}$

${\displaystyle \int log(1+x)dx=xlog(1+x)-\int (1-{\frac {1}{1+x}})dx\!}$

${\displaystyle \int log(1+x)dx=xlog(1+x)-x+log(1+x)+C\!}$

Therefore: