Trigonometry/Functions

• See also Trigonometry/Polar for an approach that is useful for -∞<θ<∞

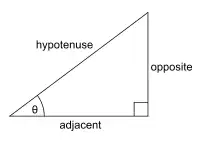
There are six trigonometric functions in Trigonometry: sine, cosine, tangent, cotangent, secant, and cosecant.

• Sine θ is the length of the leg opposite θ over the length of the hypotenuse: ${\displaystyle \sin \theta ={\frac {opp}{hyp}}}$

• Cosine θ is the length of the leg adjacent to θ over the hypotenuse: ${\displaystyle \cos \theta ={\frac {adj}{hyp}}}$

• Tangent of θ is the length of the leg on the opposite side of the triangle from the angle θ over the length of the leg of the triangle adjacent to the angle θ: ${\displaystyle \tan \theta ={\frac {opp}{adj}}}$

These three can be memorized by use of the name of the princess "Soh Cah Toa," meaning:

• "sine-opposite-hypotenuse
• cosine-adjacent-hypotenuse
• tangent-opposite-adjacent".

The remaining ratios are reciprocals of the previous ratios:

• Cotangent θ is the reciprocal of tangent θ: ${\displaystyle \cot \theta ={\frac {adj}{opp}}}$

• Secant θ is the reciprocal of cosine θ: ${\displaystyle \sec \theta ={\frac {hyp}{adj}}}$

• Cosecant θ is the reciprocal of sine θ: ${\displaystyle \csc \theta ={\frac {hyp}{opp}}}$

• Since the hypotenuse of a right triangle is always the longest side, ${\displaystyle opp<hyp\,}$ and ${\displaystyle adj<hyp\,}$
• If we divide both sides of each of these inequalities by the positive number ${\displaystyle hyp\,}$, we get ${\displaystyle {\frac {opp}{hyp}}<{\frac {hyp}{hyp}}\,}$ and ${\displaystyle {\frac {adj}{hyp}}<{\frac {hyp}{hyp}}\,}$
  or ${\displaystyle \sin \theta \leq 1\,}$ and ${\displaystyle \cos \theta \leq 1\,}$

• Trigonometry/Functions/Quiz

• Reading: w:Trigonometric_Functions (Wikipedia)
• Videos:

Basic Trigonometry (Youtube)

Basic Trigonometry II (Youtube)

• Trigonometry/Functions/Flash cards