Euler-Bernoulli Beam
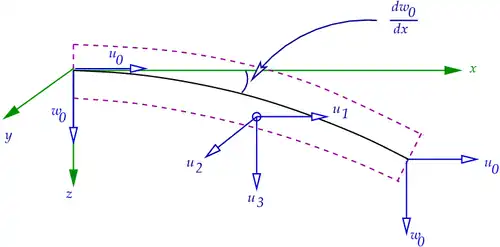 Euler-Bernoulli beam Euler-Bernoulli beam |
Displacements

Strains


Strain-Displacement Relations


The displacements

The derivatives

von Karman strains
The von Karman strains
![{\displaystyle {\begin{aligned}\varepsilon _{11}&={\cfrac {du_{0}}{dx_{1}}}-x_{3}{\cfrac {d^{2}w_{0}}{dx_{1}^{2}}}+{\frac {1}{2}}\left[\left({\cfrac {du_{0}}{dx_{1}}}-x_{3}{\cfrac {d^{2}w_{0}}{dx_{1}^{2}}}\right)^{2}+\left({\cfrac {dw_{0}}{dx_{1}}}\right)^{2}\right]\\\varepsilon _{22}&=0\\\varepsilon _{33}&={\frac {1}{2}}\left({\cfrac {dw_{0}}{dx_{1}}}\right)^{2}\\\varepsilon _{23}&=0\\\varepsilon _{31}&={\frac {1}{2}}\left({\cfrac {dw_{0}}{dx_{1}}}-{\cfrac {dw_{0}}{dx_{1}}}\right)-{\frac {1}{2}}\left[\left({\cfrac {du_{0}}{dx_{1}}}-x_{3}{\cfrac {d^{2}w_{0}}{dx_{1}^{2}}}\right)\left({\cfrac {dw_{0}}{dx_{1}}}\right)\right]\\\varepsilon _{12}&=0\end{aligned}}}](../a21b537e2ea75e84391480ff4da1f5a3f5aaf967.svg)
Equilibrium Equations
Balance of forces

Stress Resultants

Constitutive Relations
Stress-Strain equation

Stress Resultant - Displacement relations
![{\displaystyle {\begin{aligned}N_{xx}&=A_{xx}\varepsilon _{xx}^{0}+B_{xx}\varepsilon _{xx}^{1}=A_{xx}\left[{\cfrac {du_{0}}{dx}}+{\frac {1}{2}}\left({\cfrac {dw_{0}}{dx}}\right)^{2}\right]-B_{xx}{\cfrac {d^{2}w_{0}}{dx^{2}}}\\M_{xx}&=B_{xx}\varepsilon _{xx}^{0}+D_{xx}\varepsilon _{xx}^{1}=B_{xx}\left[{\cfrac {du_{0}}{dx}}+{\frac {1}{2}}\left({\cfrac {dw_{0}}{dx}}\right)^{2}\right]-D_{xx}{\cfrac {d^{2}w_{0}}{dx^{2}}}\end{aligned}}}](../09e134796671c8d4bf39a1a7ed5e4fac40e0d4ff.svg)
Axial Equation
![{\displaystyle {\begin{aligned}\int _{x_{a}}^{x_{b}}{\cfrac {d(\delta u_{0})}{dx}}\left[{\cfrac {du_{0}}{dx}}+{\frac {1}{2}}\left({\cfrac {dw_{0}}{dx}}\right)^{2}\right]A_{xx}~dx&=\int _{x_{a}}^{x_{b}}(\delta u_{0})f~dx+\\&\delta u_{0}(x_{a})Q_{1}+\delta u_{0}(x_{b})Q_{4}\end{aligned}}}](../9e6cb90b2907d59be6976f3f4a0b2e67ca7944d2.svg)
where

Bending Equation
![{\displaystyle {\begin{aligned}\int _{x_{a}}^{x_{b}}\left\{{\cfrac {d(\delta w_{0})}{dx}}\right.&\left[{\cfrac {du_{0}}{dx}}+{\cfrac {1}{2}}~\left({\cfrac {dw_{0}}{dx}}\right)^{2}\right]{\cfrac {dw_{0}}{dx}}A_{xx}+\left.{\cfrac {d^{2}(\delta w_{0})}{dx^{2}}}\left({\cfrac {d^{2}w_{0}}{dx^{2}}}\right)D_{xx}\right\}~dx=\\&\int _{x_{a}}^{x_{b}}(\delta w_{0})q~dx+\delta w_{0}(x_{a})Q_{2}+\delta w_{0}(x_{b})Q_{5}+\delta \theta (x_{a})Q_{3}+\delta \theta (x_{b})Q_{6}~.\end{aligned}}}](../13315a5aae21e0bdb3fc1eedd4d3f2fe689b09e4.svg)
where
![{\displaystyle {\begin{aligned}\delta w_{0}&:=v_{2}&\delta \theta &:={\cfrac {dv_{2}}{dx}}\\Q_{2}&:=-\left[{\cfrac {dM_{xx}}{dx}}+N_{xx}{\cfrac {dw_{0}}{dx}}\right]_{x_{a}}&Q_{5}&:=\left[{\cfrac {dM_{xx}}{dx}}+N_{xx}{\cfrac {dw_{0}}{dx}}\right]_{x_{b}}\\Q_{3}&:=-M_{xx}(x_{a})&Q_{6}&:=M_{xx}(x_{b})\end{aligned}}}](../c10c5324568f9e62a1216ac98ddbe5ebf7438531.svg)
Finite Element Model
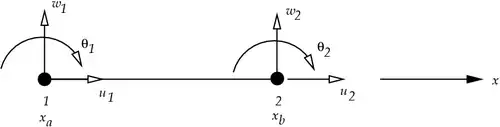 Finite element model for Euler Bernoulli beam Finite element model for Euler Bernoulli beam |

where  .
.
Hermite Cubic Shape Functions
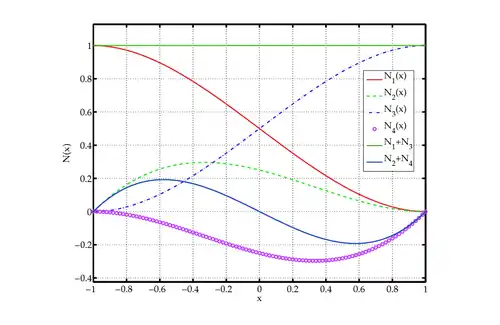 Hermite shape functions for beam Hermite shape functions for beam |
Finite Element Equations

where
![{\displaystyle {\begin{aligned}\mathbf {u} &=[u_{1}\quad u_{2}]^{T}\\\mathbf {d} &=[w_{1}\quad \theta _{1}\quad w_{2}\quad \theta _{2}]^{T}\end{aligned}}}](../411d9c55d69d78c56b388005af2fcc0c2f7860c2.svg)

Symmetric Stiffness Matrix
![{\displaystyle {\begin{aligned}K_{ij}^{11}&=\int _{x_{a}}^{x_{b}}A_{xx}{\cfrac {d\psi _{i}}{dx}}{\cfrac {d\psi _{j}}{dx}}~dx\\K_{ij}^{12}&={\frac {1}{2}}\int _{x_{a}}^{x_{b}}\left(A_{xx}{\cfrac {dw_{0}}{dx}}\right){\cfrac {d\psi _{i}}{dx}}{\cfrac {d\phi _{j}}{dx}}~dx\\K_{ij}^{21}&={\frac {1}{2}}\int _{x_{a}}^{x_{b}}\left(A_{xx}{\cfrac {dw_{0}}{dx}}\right){\cfrac {d\phi _{i}}{dx}}{\cfrac {d\psi _{j}}{dx}}~dx\\K_{ij}^{22}&=\int _{x_{a}}^{x_{b}}\left\{{\frac {1}{2}}A_{xx}\left[{\cfrac {du_{0}}{dx}}+\left({\cfrac {dw_{0}}{dx}}\right)^{2}\right]{\cfrac {d\phi _{i}}{dx}}{\cfrac {d\phi _{j}}{dx}}+D_{xx}{\cfrac {d^{2}\phi _{i}}{dx^{2}}}{\cfrac {d^{2}\phi _{j}}{dx^{2}}}\right\}~dx\end{aligned}}}](../5b56a59bc9b53f9a98d0d75c41d6f10d49cf2df4.svg)
Load Vector

Newton-Raphson Solution

where

The residual is

For Newton iterations, we use the algorithm

where the tangent stiffness matrix is given by

Tangent Stiffness Matrix
![{\displaystyle {\begin{aligned}i=1\dots 2;~j=1\dots 2&:\\&{T_{ij}^{11}=K_{ij}^{11}}\\\\i=1\dots 2;~j=1\dots 4&:\\&{T_{ij}^{12}=2K_{ij}^{12}}\\\\i=1\dots 4;~j=1\dots 2&:\\&{T_{ij}^{21}=2K_{ij}^{21}}\\\\i=1\dots 4;~j=1\dots 4&:\\&{T_{ij}^{22}=K_{ij}^{22}+{\frac {1}{2}}\int _{x_{a}}^{x_{b}}A_{xx}\left[{\cfrac {du_{0}}{dx}}+2\left({\cfrac {dw_{0}}{dx}}\right)^{2}\right]{\cfrac {d\phi _{i}}{dx}}{\cfrac {d\phi _{j}}{dx}}~dx}\end{aligned}}}](../f2b3ce0ac52051a90d8fed30a8e9fea5e3b348da.svg)
Membrane Locking
Recall

where
![{\displaystyle {\begin{aligned}K_{ij}^{11}&=\int _{x_{a}}^{x_{b}}A_{xx}{\cfrac {d\psi _{i}}{dx}}{\cfrac {d\psi _{j}}{dx}}~dx\\K_{ij}^{12}&={\frac {1}{2}}\int _{x_{a}}^{x_{b}}\left(A_{xx}{\cfrac {dw_{0}}{dx}}\right){\cfrac {d\psi _{i}}{dx}}{\cfrac {d\phi _{j}}{dx}}~dx\\K_{ij}^{21}&={\frac {1}{2}}\int _{x_{a}}^{x_{b}}\left(A_{xx}{\cfrac {dw_{0}}{dx}}\right){\cfrac {d\phi _{i}}{dx}}{\cfrac {d\psi _{j}}{dx}}~dx\\K_{ij}^{22}&=\int _{x_{a}}^{x_{b}}\left\{{\frac {1}{2}}A_{xx}\left[{\cfrac {du_{0}}{dx}}+\left({\cfrac {dw_{0}}{dx}}\right)^{2}\right]{\cfrac {d\phi _{i}}{dx}}{\cfrac {d\phi _{j}}{dx}}+D_{xx}{\cfrac {d^{2}\phi _{i}}{dx^{2}}}{\cfrac {d^{2}\phi _{j}}{dx^{2}}}\right\}~dx\end{aligned}}}](../5b56a59bc9b53f9a98d0d75c41d6f10d49cf2df4.svg)
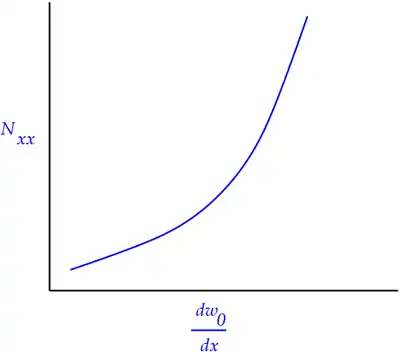
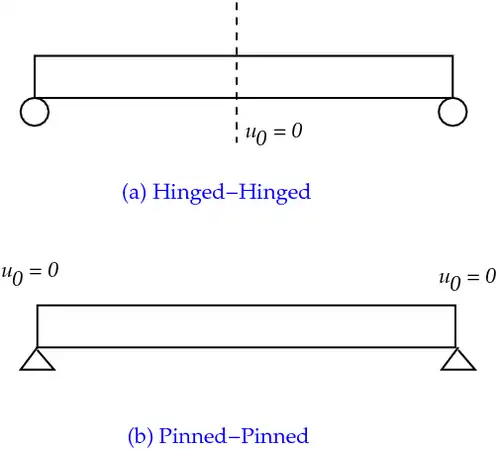 Mebrane locking in Euler-Bernoulli beam Mebrane locking in Euler-Bernoulli beam |
For Hinged-Hinged
Membrane strain:

or

Hence, shape functions should be such that

 linear,
linear,  cubic
cubic  Element Locks!
Too stiff.
Element Locks!
Too stiff.