Linear algebra (Osnabrück 2024-2025)/Part II/Lecture 52

On ${}\mathbb {R} ^{n}$ , there are several norms; however, many important concepts like the convergence of a sequence, the compactness of a subset, the continuity of a mapping, do not depend on the norm nut only on the topology. This means that we can often choose a norm that is particularly adapted for a certain problem. In this lecture we discuss the topological basics for this approach; we will usually skip the proofs, which can be found in an appendix. In the next two lectures we will apply these methods to understand the convergence of powers of matrices.

Subsets in a metric space

The form of a ball depends on the norm and on the metric.

Definition

Let ${}(M,d)$ be a metric space, ${}x\in M$ , and ${}\epsilon >0$ a positive real number. Then

{}U{\left(x,\epsilon \right)}={\left\{y\in M\mid d(x,y)<\epsilon \right\}}\,

is called the open ball, and

{}B\left(x,\epsilon \right)={\left\{y\in M\mid d(x,y)\leq \epsilon \right\}}\,

is called the closed ball

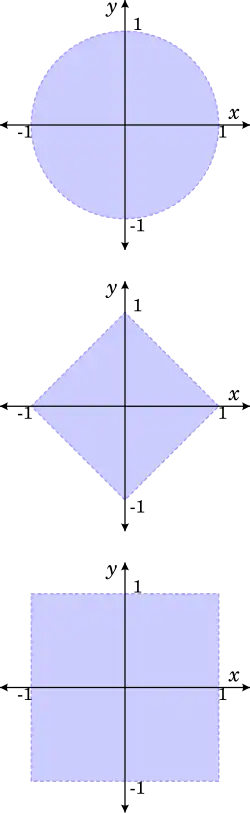
around

{}x

of radius

{}\epsilon

.

Balls do not necessarily look like a ball, they do however in the Euclidean norm. For ${}x\in \mathbb {R}$ , ${}U{\left(x,\epsilon \right)}$ is just the open interval ${}]x-\epsilon ,x+\epsilon [$ , and ${}B\left(x,\epsilon \right)$ is just the closed interval ${}[x-\epsilon ,x+\epsilon ]$ .

A subset is open if every point in it has an open ball neighborhood around it in the subset. For such a set it is decisive whether the *boundary points* belong to the set or no.

Definition

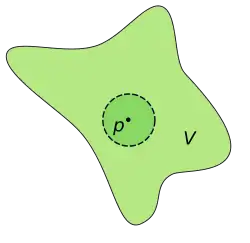
Let ${}(M,d)$ be a metric space. A subset ${}U\subseteq M$ is called open (in $(M,d)$ ), if for every ${}x\in U$ there exists an ${}\epsilon >0$ such that

{}U{\left(x,\epsilon \right)}\subseteq U\,

holds.

Definition

Let ${}(M,d)$ be a metric space. A subset ${}A\subseteq M$ is called closed if the complement ${}M\setminus A$ is

open.

Caution! Closed is not the "opposite“ of open. "Most“ subsets of a metric space are neither open nor closed; there are also some subsets that are both open and closed, e.g., the empty subset and the total space. Open balls are indeed open, and closed balls are indeed closed, see Exercise 52.1 and Exercise 52.2 .

Lemma

Let ${}(M,d)$ be a

metric space. Then the following properties hold.

The empty set ${}\emptyset$ and the total space ${}M$ are open.
Let ${}I$ be an arbitrary index set, and let ${}U_{i}$ , ${}i\in I$ , denote open sets. Then also the union
$\bigcup _{i\in I}U_{i}$

is open.
Let ${}I$ be a finite index set, and let ${}U_{i}$ , ${}i\in I$ , be open sets. Then also the intersection
$\bigcap _{i\in I}U_{i}$

is open.

Proof

See Exercise 52.4 .

\Box

Therefore, the open sets in a metric space form a topology in the sense of the following definition.

Definition

A topological space ${}(X,{\mathcal {T}})$ consists of a set ${}X$ together with a subset ${}{\mathcal {T}}$ of the power set of ${}X$ that satisfies the following structural conditions (the subsets ${}U\subseteq X$ belonging to ${}{\mathcal {T}}$ are called open).

The empty set and the set ${}X$ are open.
The intersection of finitely many open sets is again open; that is, if ${}U_{1},\ldots ,U_{n}\in {\mathcal {T}}$ , then also ${}U_{1}\cap \ldots \cap U_{n}\in {\mathcal {T}}$ .
The union of arbitrary many open sets is again open; that is, if ${}U_{i}\in {\mathcal {T}}$ for every ${}i\in I$ (of an arbitrary index set ${}I$ ), then also ${}\bigcup _{i\in I}U_{i}\in {\mathcal {T}}$ .

Equivalent norms

Definition

Let ${}V$ be a ${}{\mathbb {K} }$ -vector space. Two norms ${}\Vert {-}\Vert _{1}$ and ${}\Vert {-}\Vert _{2}$ are called equivalent, if they define the same topology, that is, the same

open sets.

Example

On ${}\mathbb {R} ^{n}$ , the Euclidean norm, the sum norm, and the maximum norm are equivalent. To see this, let ${}x=\left(x_{1},\,\ldots ,\,x_{n}\right)\in \mathbb {R} ^{n}$ be a vector, and assume without loss of generality that ${}x_{1}$ has the largest modulus among the components. Then we have the the estimates

{}\Vert {x}\Vert _{\rm {max}}=\vert {x_{1}}\vert ={\sqrt {x_{1}^{2}}}\leq {\sqrt {x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}}}\leq {\sqrt {nx_{1}^{2}}}={\sqrt {n}}\vert {x_{1}}\vert ={\sqrt {n}}\Vert {x}\Vert _{\rm {max}}\,,

and this yields essentially the equivalence between the Euclidean norm and the maximum norm.

We will see in Theorem 52.16 that on a finite-dimensional ${}{\mathbb {K} }$ -vector space, and two norms are equivalent. In order to see this, we need some preparations, in particular, the concept of compactness.

Compactness

Definition

A subset ${}T\subseteq M$ in a metric space ${}M$ is called bounded if there exists a real number ${}b$ satisfying

d{\left(x,y\right)}\leq b{\text{ for all }}x,y\in T.

Definition

A subset ${}T\subseteq \mathbb {R} ^{m}$ is called compact if it is closed and

bounded.

The boundedness and also compactness depend on the chosen metric. It is important to also have a notion of compactness that is purely topological.

Definition

A topological space ${}X$ is called compact if for every open covering

X=\bigcup _{i\in I}U_{i}\,\,\,{\text{ with }}U_{i}{\text{ open and }}I{\text{ an arbitrary index set}},

there exists a finite subset ${}J\subseteq I$ such that

{}X=\bigcup _{i\in J}U_{i}\,

holds.

The following theorem is called Theorem of Heine-Borel.

Theorem

Let ${}T\subseteq \mathbb {R} ^{n}$

be a subset. Then the following statements are equivalent.

${}T$ is compact.
Every sequence ${}{\left(x_{n}\right)}_{n\in \mathbb {N} }$ in ${}T$ has an accumulation point in ${}T$ .
Every sequence ${}{\left(x_{n}\right)}_{n\in \mathbb {N} }$ in ${}T$ has a subsequence that converges in ${}T$ .
${}T$ is closed and bounded.

Continuous mappings between metric spaces

A metric space is given by a distance function; this implies that two points might be "closer“ to each other than two other points. For a mapping

f\colon L\longrightarrow M

between two metric spaces, one can ask to what extent it is possible to control the distance in the target space ${}M$ by the distance in the source space ${}L$ . Let ${}x\in L$ , and let ${}y=f(x)$ denote the image point. One would like that for a point ${}x'\in L$ , that is "close“ to ${}x$ , also the image point ${}f(x')$ is close to ${}f(x)$ . In order to make this intuitive idea more precise, let ${}\epsilon >0$ be given. This ${}\epsilon$ represents a "accuracy wished for“. The question is whether there exists a ${}\delta >0$ (a "starting accuracy“) such that for all ${}x'$ fulfilling ${}d{\left(x,x'\right)}\leq \delta$ , the relation ${}d{\left(f(x),f(x')\right)}\leq \epsilon$ holds. This leads to the concept of a continuous mapping.

Definition

Let ${}(L,d_{1})$ and ${}(M,d_{2})$ be metric spaces,

f\colon L\longrightarrow M

a mapping, and ${}x\in L$ . The mapping ${}f$ is called continuous in ${}x$ if for every ${}\epsilon >0$ there exists a ${}\delta >0$ such that

{}f{\left(B\left(x,\delta \right)\right)}\subseteq B\left(f(x),\epsilon \right)\,

holds. The mapping ${}f$ is called continuous if it is continuous in ${}x$ for every

{}x\in L

.

Instead of working with closed ball neighborhoods, we could work with open ball neighborhoods. The easiest examples of continuous mappings are a constant mapping, the identity of a metric space, and the inclusion ${}T\subseteq M$ of a subset of a metric space, endowed with the induced metric. See the exercises.

Theorem

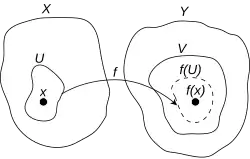
Let

f\colon L\longrightarrow M,x\longmapsto f(x),

denote a mapping between the metric spaces

{}L

and

{}M

. Then the following statements are equivalent.

${}f$ is continuous in every point ${}x\in L$ .
For every point ${}x\in L$ and every ${}\epsilon >0$ , there exists a ${}\delta >0$ such that ${}d(x,x')\leq \delta$ implies that ${}d(f(x),f(x'))\leq \epsilon$ holds.
For every point ${}x\in L$ and every convergent sequence ${}{\left(x_{n}\right)}_{n\in \mathbb {N} }$ in ${}L$ with ${}\lim _{n\rightarrow \infty }x_{n}=x$ , also the image sequence ${}{\left(f(x_{n})\right)}_{n\in \mathbb {N} }$ converges to the limit ${}f(x)$ .
For every open set ${}V\subseteq M$ , also the preimage ${}f^{-1}(V)$ is open.

The property (4) shows that continuity is purely a topological property.

Linear continuous mappings

A linear mapping is in general not continuous. However, there is a quite simple characterization for continuity of a linear mapping, it is enough to check continuity in the origin. We will see in Theorem 52.17 that this property does always hold for finite-dimensional vector spaces.

Theorem

Let ${}V$ and ${}W$ be normed ${}{\mathbb {K} }$ -vector spaces, and let

\varphi \colon V\longrightarrow W

denote a

linear mapping. Then the following properties are equivalent.

${}\varphi$ is continuous.
${}\varphi$ is continuous in the origin.
The set
${\left\{\varphi (v)\mid v\in V,\,\Vert {v}\Vert =1\right\}}$

is bounded.

Proof

From (1) to (2) is clear. From (2) to (3). In particular, there exists for ${}\epsilon =1$ a ${}\delta >0$ such that

{}\Vert {v}\Vert \leq \delta \,

implies the estimate

{}\Vert {\varphi (v)}\Vert \leq 1\,.

Therefore,

{}\Vert {v}\Vert \leq 1\,

implies then, due to the compatibility with scalars,

{}\Vert {\varphi (v)}\Vert \leq {\frac {1}{\delta }}\,.

From (3) to (1). Let ${}C$ be an upper bound for the norm on the image set of the ${}1$ -sphere. Let ${}v\in V$ be given. We have

{}{\begin{aligned}d(\varphi (v),\varphi (w))&=\Vert {\varphi (v)-\varphi (w)}\Vert \\&=\Vert {\varphi (v-w)}\Vert \\&=\Vert {v-w}\Vert \cdot \Vert {\varphi {\left({\frac {(v-w)}{\Vert {v-w}\Vert }}\right)}}\Vert \\&\leq \Vert {v-w}\Vert \cdot C.\end{aligned}}

Hence, for ${}\epsilon >0$ , we can choose

{\displaystyle {}\delta

\Box

Equivalence of norms

Lemma

Let ${}V$ be a ${}{\mathbb {K} }$ -vector space, and let ${}\Vert {-}\Vert _{1}$ and ${}\Vert {-}\Vert _{2}$ be norms

on

{}V

. Then the following statements are equivalent.

The two norms are equivalent.
The identity
$V\longrightarrow V$

is continuous when ${}V$ is endowed with the first norm on the left, and the second norm on the right, and vice versa.
The ${}\Vert {-}\Vert _{1}$ -ball is bounded with respect to the ${}\Vert {-}\Vert _{2}$ -norm, and vice versa.
There exist real numbers ${}a,b$ such that
${}\Vert {v}\Vert _{2}\leq a\Vert {v}\Vert _{1}\,$

and

${}\Vert {v}\Vert _{1}\leq b\Vert {v}\Vert _{2}\,$

holds for all ${}v\in V$ .

Proof

The equivalence between (1) and (2) follows from Theorem 52.13 , the equivalence between (2) and (3) follows from Theorem 52.14 . The properties (3) and (4) are equivalent due to the compatibility of the norms with scalars.

\Box

Theorem

On a finite-dimensional ${}{\mathbb {K} }$ -vector space ${}V$ , any two norms are

equivalent.

Proof

We use Lemma 52.15 . The norm and the topology depend only on the underlying real vector space; therefore, we may assume

{}{\mathbb {K} }=\mathbb {R} \,,

For a basis ${}v_{1},\ldots ,v_{n}\in V$ , there exists an isomorphism

\varphi \colon \mathbb {R} ^{n}\longrightarrow V

with ${}e_{i}\mapsto v_{i}$ . Under an isomorphism ${}\varphi$ , by setting

{}\Vert {u}\Vert ':=\Vert {\varphi (u)}\Vert \,

we get a norm on ${}\mathbb {R} ^{n}$ . Hence, we may directly consider the case ${}V=\mathbb {R} ^{n}$ . We compare now an arbitrary norm on ${}\mathbb {R} ^{n}$ with the maximum norm and with the Euclidean norm; we know by Example 52.7 that these two norms are equivalent to each other. Let ${}v=\sum _{i=1}^{n}a_{i}e_{i}$ . Because of

{}{\begin{aligned}\Vert {v}\Vert &=\Vert {\sum _{i=1}^{n}a_{i}e_{i}}\Vert \\&\leq \sum _{i=1}^{n}\Vert {a_{i}e_{i}}\Vert \\&=\sum _{i=1}^{n}\vert {a_{i}}\vert \cdot \Vert {e_{i}}\Vert \\&\leq n\cdot {\max {\left(\Vert {e_{i}}\Vert ,i=1,\ldots ,n\right)}}\Vert {v}\Vert _{\rm {max}},\end{aligned}}

sufficiently small ${}\Vert {-}\Vert _{\rm {max}}$ -open balls are contained in ${}\Vert {-}\Vert$ -open balls. Therefore, the topology of the maximum norm is as fine as the topology of any other norm. To prove the converse, we consider the identity

\mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{n},

where the topology on the left-hand side is given by the Euclidean norm (or maximum norm), and on the right-hand side by the norm. The reasoning so far shows that this mapping is continuous. The Euclidean ${}1$ -sphere ${}S$ on the left is compact due to the theorem of Heine-Borel

and, according to Fact *****, ${}S$ is also compact with respect to the norm ${}\Vert {-}\Vert$ . We denote this set by ${}S'$ . Since ${}\mathbb {R} ^{n}$ is a Hausdorff-space with every norm, it follows by Exercise 52.5 that ${}S'$ is closed. Since the origin does not belong to ${}S'$ , there exists a

{}\delta >0\,

such that

{}U{\left(0,\delta \right)}\cap S'=\emptyset \,

(the open ball with respect to $\Vert {-}\Vert$ ). For ${}v\neq 0$ we obtain, because of ${}{\frac {v}{\Vert {v}\Vert _{\rm {Euc}}}}\in S=S'$ , the estimate

{}\Vert {\frac {v}{\Vert {v}\Vert _{\rm {Euc}}}}\Vert \geq \delta \,.

Therefore,

{}\Vert {v}\Vert _{\rm {Euc}}\leq {\frac {1}{\delta }}\Vert {v}\Vert \,.

\Box

Theorem

Let ${}V$ and ${}W$ be normed ${}{\mathbb {K} }$ -vector spaces, and let

\varphi \colon V\longrightarrow W

denote a linear mapping. Let ${}V$ be finite-dimensional. Then ${}\varphi$ is

continuous.

Proof

The image under the mapping is also a finite-dimensional vector space; therefore, we may assume that both spaces are finite-dimensional. We also may assume that ${}V=\mathbb {R} ^{n}$ and ${}W=\mathbb {R} ^{m}$ . Because of Theorem 52.16 , we may assume that we have the maximum norm on both sides. Let ${}a$ be the maximum of the absolute values of the entries in the describing matrix ${}M={\left(a_{ij}\right)}_{ij}$ of ${}\varphi$ , with respect to the standard bases. For ${}v\in \mathbb {R} ^{n}$ with

{}\Vert {v}\Vert _{\rm {max}}\leq 1\,,

we obtain

{}\Vert {\varphi (v)}\Vert _{\rm {max}}=\Vert {\begin{pmatrix}\sum _{j=1}^{n}a_{1j}v_{j}\\\vdots \\\sum _{j=1}^{n}a_{nj}v_{j}\end{pmatrix}}\Vert _{\rm {max}}={\max {\left(\vert {\sum _{j=1}^{n}a_{ij}v_{j}}\vert ,i=1,\ldots ,m\right)}}\leq na\,.

Therefore, continuity follows from Theorem 52.14 .

\Box

<< \| Linear algebra (Osnabrück 2024-2025)/Part II \| >> PDF-version of this lecture Exercise sheet for this lecture (PDF)