Linear algebra (Osnabrück 2024-2025)/Part II/Lecture 43

For a quadratic polynomial ${\displaystyle {}aX^{2}+bX+c}$ in one variable ${\displaystyle {}X}$, with ${\displaystyle {}a,b,c\in K}$ and ${\displaystyle {}a\neq 0}$, the zeroes can be found by completing the square. That is, we write (suppose that the characteristic of the fields is not ${\displaystyle {}2}$)

${\displaystyle {}aX^{2}+bX+c=a{\left(X^{2}+{\frac {b}{a}}X+{\frac {c}{a}}\right)}=a{\left({\left(X+{\frac {b}{2a}}\right)}^{2}-{\frac {b^{2}}{4a^{2}}}+{\frac {c}{a}}\right)}\,.}$

This equals ${\displaystyle {}0}$ if and only if

${\displaystyle {}X=\pm {\sqrt {{\frac {b^{2}}{4a^{2}}}-{\frac {c}{a}}}}-{\frac {b}{2a}}\,,}$

and if the square root

${\displaystyle {}{\sqrt {{\frac {b^{2}}{4a^{2}}}-{\frac {c}{a}}}}={\frac {1}{2a}}{\sqrt {b^{2}-4ac}}\,}$

exists in the field. Depending on this, there are no, one or two solutions.

We make a list of real quadratic polynomials in the two variables ${\displaystyle {}X}$ and ${\displaystyle {}Y}$, together with their corresponding vanishing sets; we restrict to coefficients from ${\displaystyle {}0,1,-1}$. If only one variable ${\displaystyle {}X}$ occurs, then we have essentially the following three possibilities.

• ${\displaystyle {}X^{2}\,}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ the vanishing set is a "doubled line“.
• ${\displaystyle {}X^{2}-1\,}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ this means

${\displaystyle {}X=\pm 1}$, the vanishing set consists in two parallel lines.

• ${\displaystyle {}X^{2}+1\,}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ the vanishing set is leer.

In these cases (where the second variable ${\displaystyle {}Y}$ does not occur explicitly), the vanishing set is simply the product set of a zero-dimensional vanishing set (finitely many points) and of a line.

Now we consider polynomials where both variables occur.

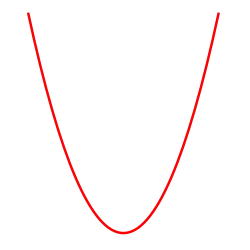
• ${\displaystyle {}Y^{2}-X\,}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ the vanishing set is a parabola.
• ${\displaystyle {}Y^{2}-X^{2}\,}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ this means

${\displaystyle {}(Y-X)(Y+X)=0}$, the vanishing set consists in two lines crossing each other.

• ${\displaystyle {}Y^{2}+X^{2}\,}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ the only solution is the point ${\displaystyle {}(0,0)}$, the vanishing set is just a single point.
• ${\displaystyle {}Y^{2}-X^{2}-1\,}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ this means

${\displaystyle {}(Y-X)(Y+X)=1}$, the vanishing set is a hyperbola.

• ${\displaystyle {}Y^{2}+X^{2}-1\,}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ the vanishing sets is the unit circle.
• ${\displaystyle {}Y^{2}+X^{2}+1\,}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ again, this is empty.

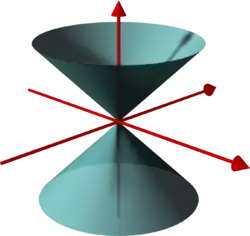
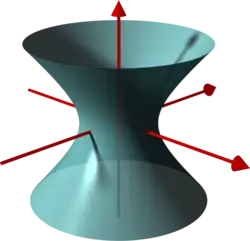
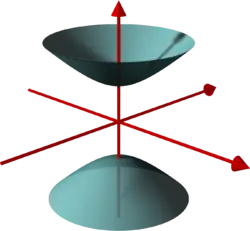
We make a list of real quadratic polynomials in the three variables ${\displaystyle {}X,Y}$ and ${\displaystyle {}Z}$, together with their corresponding vanishing sets, where we restrict the coefficients to ${\displaystyle {}0,1,-1}$. Moreover, we consider only such polynomials where all variables occur and the vanishing set is not empty.

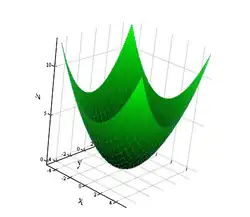
• ${\displaystyle {}Y^{2}+X^{2}-Z\,}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ the vanishing set is a paraboloid.
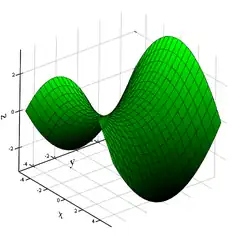
• ${\displaystyle {}Y^{2}-X^{2}-Z\,}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ the vanishing set is a saddle surface.
• ${\displaystyle {}X^{2}+Y^{2}+Z^{2}}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ the only solution is the point ${\displaystyle {}(0,0,0)}$, the vanishing set is just one point.
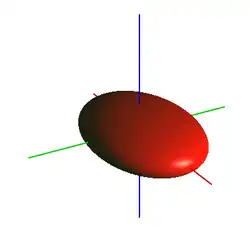
• ${\displaystyle {}X^{2}+Y^{2}+Z^{2}-1}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ the vanishing set is a sphere, that is, the surface of a ball.
• ${\displaystyle {}X^{2}+Y^{2}-Z^{2}}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ the vanishing set is the solution set of the equation

${\displaystyle {}Z^{2}=X^{2}+Y^{2}}$. This is a (double)-cone.

• ${\displaystyle {}X^{2}+Y^{2}-Z^{2}-1}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ the vanishing set is a one-sheeted hyperboloid.
• ${\displaystyle {}X^{2}+Y^{2}-Z^{2}+1}$ ${\displaystyle {}\,}$ ${\displaystyle {}\,}$ the vanishing set is a two-sheeted hyperboloid.

We consider the pure-quadratic polynomial

${\displaystyle {}F=3X^{2}-4XY+5Y^{2}\,.}$

In order to apply Theorem 43.10 , we have to find the eigenvalues of the matrix

${\displaystyle {}M={\begin{pmatrix}3&-2\\-2&5\end{pmatrix}}\,.}$

The characteristic polynomial is

${\displaystyle {}(X-3)(X-5)-4=X^{2}-8X+11=(X-4)^{2}-5\,.}$

Therefore, the eigenvalues are

${\displaystyle x_{1}={\sqrt {5}}+4{\text{ and }}x_{2}=-{\sqrt {5}}+4.}$

Therefore, in a suitable orthonormal basis, the polynomial has the form

${\displaystyle {}F={\left({\sqrt {5}}+4\right)}U^{2}+{\left(-{\sqrt {5}}+4\right)}V^{2}\,.}$

We want to bring the pure-quadratic form

${\displaystyle {\frac {3}{2}}X^{2}+2Y^{2}+2XY-2YZ}$

into a standard form in the sense of Theorem 43.10 . The corresponding symmetric matrix is

${\displaystyle {\begin{pmatrix}{\frac {3}{2}}&1&0\\1&2&-1\\0&-1&0\end{pmatrix}}.}$

We have to determine the eigenvalues of this matrix. The characteristic polynomial of the matrix is

${\displaystyle {}{\begin{aligned}\det {\begin{pmatrix}X-{\frac {3}{2}}&-1&0\\-1&X-2&1\\0&1&X\end{pmatrix}}&={\left(X-{\frac {3}{2}}\right)}{\left(X^{2}-2X-1\right)}-X\\&=X^{3}-{\frac {7}{2}}X^{2}+X+{\frac {3}{2}}\\&=(X-1){\left(X^{2}-{\frac {5}{2}}X-{\frac {3}{2}}\right)}\\&=(X-1)(X-3){\left(X+{\frac {1}{2}}\right)};\end{aligned}}}$

hence, the eigenvalues are

${\displaystyle 1,3,-{\frac {1}{2}}.}$

In the new variables ${\displaystyle {}U,V,W}$ for an orthonormal basis consisting of eigenvectors to these eigenvalues, we have

${\displaystyle {}F=U^{2}+3V^{2}-{\frac {1}{2}}W^{2}\,.}$

A quadratic form in standard form

${\displaystyle \sum _{1\leq i\leq k}r_{i}U_{i}^{2}+s\,\,{\text{ or }}\,\,\sum _{1\leq i\leq k}r_{i}U_{i}^{2}+sU_{k+1}}$

in the sense of Theorem 43.13 can be simplified further, if we allow distortions. In the new coordinates

${\displaystyle {}Z_{i}={\sqrt {\vert {r_{i}}\vert }}U_{i}\,}$

or

${\displaystyle {}U_{i}={\frac {1}{\sqrt {\vert {r_{i}}\vert }}}Z_{i}\,}$

for ${\displaystyle {}i=1,\ldots ,k}$, the quadratic form has a representation of the form

${\displaystyle \sum _{1\leq i\leq k}\pm Z_{i}^{2}+s\,\,{\text{ or }}\,\,\sum _{1\leq i\leq k}\pm Z_{i}^{2}+sZ_{k+1},}$

the coefficients are ${\displaystyle {}1}$ or ${\displaystyle {}-1}$. This is called the normalized standard form of the quadratic form. By swapping of the variables, we may achieve that the first variables have the coefficient ${\displaystyle {}1}$, and the later variables have coefficient ${\displaystyle {}-1}$. In doing these transformations, the vanishing sets are distorted. For example, an ellipse might become a circle, or a parabola might be compressed. Since the vanishing set does not change by multiplying the form with ${\displaystyle {}-1}$, we may also assume that the number variables with coefficient ${\displaystyle {}1}$ is at least the number of variables with coefficient ${\displaystyle {}-1}$.

We consider the quadratic polynomial

${\displaystyle {}F=3X^{2}-4XY+5Y^{2}+6X+2Y-7\,,}$

and we want to transform it according to Theorem 43.13 into a standard form. In Example 43.10 we have already studied the pure-quadratic part ${\displaystyle {}3X^{2}-4XY+5Y^{2}}$ with the help of the symmetric matrix

${\displaystyle {}M={\begin{pmatrix}3&-2\\-2&5\end{pmatrix}}\,,}$

the eigenvalues are

${\displaystyle x_{1}={\sqrt {5}}+4{\text{ and }}x_{2}=-{\sqrt {5}}+4.}$

In order to transform ${\displaystyle {}F}$ itself to standard form, we need the eigenvectors, and we have to perform the change of variables explicitly. The eigenvectors are

${\displaystyle {\begin{pmatrix}-2\\{\sqrt {5}}+1\end{pmatrix}}\,\,{\text{ and }}\,\,{\begin{pmatrix}2\\{\sqrt {5}}-1\end{pmatrix}};}$

therefore,

${\displaystyle u={\frac {1}{\sqrt {10+2{\sqrt {5}}}}}{\begin{pmatrix}-2\\{\sqrt {5}}+1\end{pmatrix}}\,\,{\text{ and }}\,\,v={\frac {1}{\sqrt {10-2{\sqrt {5}}}}}{\begin{pmatrix}2\\{\sqrt {5}}-1\end{pmatrix}}}$

are an orthonormal basis consisting of eigenvectors. We have the relation

${\displaystyle {}{\begin{pmatrix}u\\v\end{pmatrix}}={\begin{pmatrix}{\frac {-2}{\sqrt {10+2{\sqrt {5}}}}}&{\frac {{\sqrt {5}}+1}{\sqrt {10+2{\sqrt {5}}}}}\\{\frac {2}{\sqrt {10-2{\sqrt {5}}}}}&{\frac {{\sqrt {5}}-1}{\sqrt {10-2{\sqrt {5}}}}}\end{pmatrix}}{\begin{pmatrix}e_{1}\\e_{2}\end{pmatrix}}\,}$

in the sense of remark *****. With den new variables ${\displaystyle {}U,V}$ we obtain according to Lemma 14.14 the relation

${\displaystyle {}{\begin{pmatrix}X\\Y\end{pmatrix}}={\begin{pmatrix}{\frac {-2}{\sqrt {10+2{\sqrt {5}}}}}&{\frac {2}{\sqrt {10-2{\sqrt {5}}}}}\\{\frac {{\sqrt {5}}+1}{\sqrt {10+2{\sqrt {5}}}}}&{\frac {{\sqrt {5}}-1}{\sqrt {10-2{\sqrt {5}}}}}\end{pmatrix}}{\begin{pmatrix}U\\V\end{pmatrix}}\,.}$

Hence, we obtain (for the pure-quadratic part, we do not have to compute anything)

${\displaystyle {}{\begin{aligned}F&=3X^{2}-4XY+5Y^{2}+6X+2Y-7\\&={\left({\sqrt {5}}+4\right)}U^{2}+{\left(-{\sqrt {5}}+4\right)}V^{2}+6{\left({\frac {-2}{\sqrt {10+2{\sqrt {5}}}}}U+{\frac {2}{\sqrt {10-2{\sqrt {5}}}}}V\right)}+2{\left({\frac {{\sqrt {5}}+1}{\sqrt {10+2{\sqrt {5}}}}}U+{\frac {{\sqrt {5}}-1}{\sqrt {10-2{\sqrt {5}}}}}\right)}V-7\\&={\left({\sqrt {5}}+4\right)}U^{2}+{\left(-{\sqrt {5}}+4\right)}V^{2}+{\frac {-10+2{\sqrt {5}}}{\sqrt {10+2{\sqrt {5}}}}}U+{\frac {10+2{\sqrt {5}}}{\sqrt {10-2{\sqrt {5}}}}}V-7.\end{aligned}}}$

By completing the square with

${\displaystyle {}U=W+{\frac {5-{\sqrt {5}}}{{\sqrt {10+2{\sqrt {5}}\,}}{\left({\sqrt {5}}+4\right)}}}\,}$

and

${\displaystyle {}V=Z+{\frac {-5-{\sqrt {5}}}{{\sqrt {10-2{\sqrt {5}}\,}}{\left(-{\sqrt {5}}+4\right)}}}\,,}$

we get

${\displaystyle {}{\begin{aligned}{\left({\sqrt {5}}+4\right)}U^{2}+{\frac {-10+2{\sqrt {5}}}{\sqrt {10+2{\sqrt {5}}}}}U&={\left({\sqrt {5}}+4\right)}W^{2}+{\frac {-10+2{\sqrt {5}}}{\sqrt {10+2{\sqrt {5}}}}}\cdot {\frac {5-{\sqrt {5}}}{{\sqrt {10+2{\sqrt {5}}\,}}{\left({\sqrt {5}}+4\right)}}}\\&={\left({\sqrt {5}}+4\right)}W^{2}-{\frac {60-20{\sqrt {5}}}{{\left(10+2{\sqrt {5}}\right)}{\left({\sqrt {5}}+4\right)}}}\,\end{aligned}}}$

and

${\displaystyle {}{\begin{aligned}{\left(-{\sqrt {5}}+4\right)}V^{2}+{\frac {10+2{\sqrt {5}}}{\sqrt {10-2{\sqrt {5}}}}}V&={\left(-{\sqrt {5}}+4\right)}Z^{2}+{\frac {10+2{\sqrt {5}}}{\sqrt {10-2{\sqrt {5}}}}}\cdot {\frac {-5-{\sqrt {5}}}{{\sqrt {10-2{\sqrt {5}}\,}}{\left(-{\sqrt {5}}+4\right)}}}\\&={\left(-{\sqrt {5}}+4\right)}Z^{2}-{\frac {60+20{\sqrt {5}}}{{\left(10-2{\sqrt {5}}\right)}{\left(-{\sqrt {5}}+4\right)}}}.\,\end{aligned}}}$

Altogether this yields

${\displaystyle {}F={\left({\sqrt {5}}+4\right)}W^{2}+{\left(-{\sqrt {5}}+4\right)}Z^{2}-{\frac {60-20{\sqrt {5}}}{{\left(10+2{\sqrt {5}}\right)}{\left({\sqrt {5}}+4\right)}}}-{\frac {60+20{\sqrt {5}}}{{\left(10-2{\sqrt {5}}\right)}{\left(-{\sqrt {5}}+4\right)}}}-7\,.}$