Linear algebra (Osnabrück 2024-2025)/Part II/Lecture 32

Orthogonality

When an inner product is given, then we can express the property of two vectors to be orthogonal to each other.

Definition

Let ${}V$ denote a vector space over ${}{\mathbb {K} }$ , endowed with an inner product ${}\left\langle -,-\right\rangle$ . We say that two vectors ${}v,w\in V$ are orthogonal (or perpendicular) to each other if

{}\left\langle v,w\right\rangle =0\,

holds.

Remark

The following reasoning shows that the orthogonality, defined via the inner product, corresponds to the intuitively given orthogonality .^[1] For orthogonal vectors ${}u,v\in V$ , we get that ${}v$ has the same distance to the points ${}u$ and ${}-u$ . This holds because of

{}{\begin{aligned}\Vert {v-u}\Vert ^{2}&=\left\langle v-u,v-u\right\rangle \\&=\left\langle v,v\right\rangle +\left\langle u,u\right\rangle \\&=\left\langle v+u,v+u\right\rangle \\&=\Vert {v+u}\Vert ^{2}.\end{aligned}}

The reverse statement holds as well; see Exercise 32.1 .

Pythagoras of Samos lived in the sixth century a.D. However, "his“ theorem was already known a thousand years earlier in Babylon.

Let us recall the Theorem of Pythagoras.

The following theorem is the Theorem of Pythagoras; more precisely, it is the version in the context of an inner product, and it is trivial. However, the relation to the classical, elementary-geometric Theorem of Pythagoras is difficult, because it is not clear at all whether our concept of orthogonality and our concept of a length, both introduced via the inner product, coincide with the corresponding intuitive concepts. That our concept of a norm is the true length concept rests itself on the Theorem of Pythagoras in a Cartesian coordinate system, which presupposes the classical theorem.

Theorem

Let ${}V$ be a ${}{\mathbb {K} }$ -vector space, endowed with an inner product ${}\left\langle -,-\right\rangle$ . Let ${}u,v\in V$ be vectors that are orthogonal to each other. Then

{}\Vert {u+v}\Vert ^{2}=\Vert {u}\Vert ^{2}+\Vert {v}\Vert ^{2}\,

holds.

Proof

We have

{}\Vert {u+v}\Vert ^{2}=\left\langle u+v,u+v\right\rangle =\left\langle u,u\right\rangle +\left\langle u,v\right\rangle +\left\langle v,u\right\rangle +\left\langle v,v\right\rangle =\Vert {u}\Vert ^{2}+\Vert {v}\Vert ^{2}\,.

\Box

Definition

Let ${}V$ be a ${}{\mathbb {K} }$ -vector space, endowed with an inner product, and let ${}U\subseteq V$ denote a linear subspace. Then

{}U^{\perp }={\left\{v\in V\mid \left\langle v,u\right\rangle =0{\text{ for  all }}u\in U\right\}}\,

is called the orthogonal complement of

{}U

.

The orthogonal complement of a linear subspace is again a linear subspace; see Exercise 32.8 . If a generating system of ${}U$ is given, then a vector ${}v\in V$ belongs to the orthogonal complement of ${}U$ if it is orthogonal to all the vectors of the generating system; see Exercise 32.9 .

Example

Let ${}V=\mathbb {R} ^{n}$ , endowed with the standard inner product. For the one-dimensional linear subspace ${}\mathbb {R} e_{i}$ , generated by the standard vector ${}e_{i}$ , the orthogonal complement consists of all vectors ${}{\begin{pmatrix}x_{1}\\\vdots \\x_{i-1}\\0\\x_{i+1}\\\vdots \\x_{n}\end{pmatrix}}$ , where the ${}i$ -th entry is ${}0$ . For a one-dimensional linear subspace ${}\mathbb {R} v$ , generated by a vector

{}v={\begin{pmatrix}a_{1}\\a_{2}\\\vdots \\a_{n}\end{pmatrix}}\neq 0\,,

the orthogonal complement can be found by determining the solution space of the linear equation

{}a_{1}x_{1}+\cdots +a_{n}x_{n}=0\,.

The orthogonal space

{}U=(\mathbb {R} v)^{\perp }={\left\{{\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}\mid a_{1}x_{1}+\cdots +a_{n}x_{n}=0\right\}}\,

has dimension ${}n-1$ ; this is a so-called hyperplane. The vector ${}v$ is called a normal vector for the hyperplane ${}U$ .

For a linear subspace ${}U\subseteq \mathbb {R} ^{n}$ that is given by a basis (or a generating system) ${}v_{i}={\begin{pmatrix}a_{i1}\\\vdots \\a_{in}\end{pmatrix}}$ , ${}i=1,\ldots ,k$ , the orthogonal complement is the solution space of the system of linear equations

{}A{\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}=0\,,

where ${}A={\left(a_{ij}\right)}$ is the matrix formed by the vectors ${}v_{i}$ as rows.

Orthonormal bases

Definition

Let ${}V$ be a ${}{\mathbb {K} }$ -vector space, endowed with an inner product. A basis ${}v_{i}$ , ${}i\in I$ , of ${}V$ is called an orthogonal basis if

\left\langle v_{i},v_{j}\right\rangle =0{\text{ for }}i\neq j

holds.

Definition

Let ${}V$ be a ${}{\mathbb {K} }$ -vector space, endowed with an inner product ${}\left\langle -,-\right\rangle$ . A basis ${}v_{i}$ , ${}i\in I$ , of ${}V$ is called an orthonormal basis if

\left\langle v_{i},v_{i}\right\rangle =1{\text{ for all }}i\in I{\text{ and }}\left\langle v_{i},v_{j}\right\rangle =0{\text{ for }}i\neq j

holds.

The elements in an orthonormal basis have norm ${}1$ , and they are orthogonal to each other. Hence, an orthonormal basis is a orthogonal basis, that also satisfies the norm condition

{}\Vert {v_{i}}\Vert ={\sqrt {\left\langle v_{i},v_{i}\right\rangle }}=1\,.

It is easy to transform an orthogonal basis to an orthonormal basis, by replacing every ${}v_{i}$ by its normalization ${}{\frac {v_{i}}{\Vert {v_{i}}\Vert }}$ (as ${}v_{i}$ is part of a basis, its norm is not ${}0$ ). A family of vectors, all of the norm ${}1$ , and orthogonal to each other, but not necessarily a basis, is called an orthonormal system.

Lemma

Let ${}V$ be a ${}{\mathbb {K} }$ -vector space, endowed with an inner product, and let ${}u_{i}$ , ${}i\in I$ , be an orthonormal basis of ${}V$ . Then the coefficients of a vector ${}v$ , with respect to this basis, are given by

{}v=\sum _{i\in I}\left\langle v,u_{i}\right\rangle u_{i}\,.

Proof

Since we have a basis, there exists a unique representation

{}v=\sum _{j\in I}a_{j}u_{j}\,

(where all ${}a_{j}$ are ${}0$ up to finitely many). Therefore, the claim follows from

{}\left\langle v,u_{i}\right\rangle =\left\langle \sum _{j\in I}a_{j}u_{j},u_{i}\right\rangle =\sum _{j\in I}a_{j}\left\langle u_{j},u_{i}\right\rangle =a_{i}\,.

\Box

We will mainly consider orthonormal bases in the finite-dimensional case. In ${}\mathbb {R} ^{n}$ , the standard basis is an orthonormal basis. In the plane ${}\mathbb {R} ^{2}$ , any orthonormal basis is of the form ${}{\begin{pmatrix}a\\b\end{pmatrix}},{\begin{pmatrix}-b\\a\end{pmatrix}}$ or of the form ${}{\begin{pmatrix}a\\b\end{pmatrix}},{\begin{pmatrix}b\\-a\end{pmatrix}}$ , where ${}a^{2}+b^{2}=1$ holds. For example, ${}{\begin{pmatrix}{\frac {3}{5}}\\{\frac {4}{5}}\end{pmatrix}},{\begin{pmatrix}-{\frac {4}{5}}\\{\frac {3}{5}}\end{pmatrix}}$ is an orthonormal basis. The following Gram–Schmidt orthonormalization describes a method to construct, starting with any basis of a finite-dimensional vector space, an orthonormal basis that generates the same flag of linear subspaces.

Theorem

Let ${}V$ be a finite-dimensional ${}{\mathbb {K} }$ -vector space, endowed with an inner product, and let ${}v_{1},v_{2},\ldots ,v_{n}$ be a basis of ${}V$ . Then there exists an orthonormal basis ${}u_{1},u_{2},\ldots ,u_{n}$ of ${}V$ with^[2]

{}\langle v_{1},v_{2},\ldots ,v_{i}\rangle =\langle u_{1},u_{2},\ldots ,u_{i}\rangle \,

for all

{}i=1,\ldots ,n

.

Proof

We prove the statement by induction over ${}i$ , that is, we construct successively a family of orthonormal vectors spanning the same linear subspaces. For ${}i=1$ , we just have to normalize ${}v_{1}$ , that is, we replace it by ${}u_{1}={\frac {v_{1}}{\Vert {v_{1}}\Vert }}$ . Now suppose that the statement is already proven for ${}i$ . Let a family of orthonormal vectors ${}u_{1},\ldots ,u_{i}$ fulfilling ${}\langle u_{1},\ldots ,u_{i}\rangle =\langle v_{1},\ldots ,v_{i}\rangle$ be already constructed. We set

w_{i+1}=v_{i+1}-\left\langle v_{i+1},u_{1}\right\rangle u_{1}-\cdots -\left\langle v_{i+1},u_{i}\right\rangle u_{i}\,.

Due to

{}{\begin{aligned}\left\langle w_{i+1},u_{j}\right\rangle &=\left\langle v_{i+1}-\left\langle v_{i+1},u_{1}\right\rangle u_{1}-\cdots -\left\langle v_{i+1},u_{i}\right\rangle u_{i},u_{j}\right\rangle \\&=\left\langle v_{i+1},u_{j}\right\rangle -\sum _{k\leq i,k\neq j}\left\langle v_{i+1},u_{k}\right\rangle \left\langle u_{k},u_{j}\right\rangle -\left\langle v_{i+1},u_{j}\right\rangle \left\langle u_{j},u_{j}\right\rangle \\&=\left\langle v_{i+1},u_{j}\right\rangle -\left\langle v_{i+1},u_{j}\right\rangle \\&=0,\end{aligned}}

this vector is orthogonal to all ${}u_{1},\ldots ,u_{i}$ , and also

{}\langle u_{1},\ldots ,u_{i},w_{i+1}\rangle =\langle v_{1},\ldots ,v_{i},v_{i+1}\rangle \,

holds. By normalizing ${}w_{i+1}$ , we obtain ${}u_{i+1}$ .

\Box

Example

Let ${}V$ be the kernel of the linear mapping

\mathbb {R} ^{3}\longrightarrow \mathbb {R} ,(x,y,z)\longmapsto 2x+3y-z.

As a linear subspace of ${}\mathbb {R} ^{3}$ , ${}V$ carries the induced inner product. We want to determine an orthonormal basis of ${}V$ . For this, we consider the basis consisting of the vectors

v_{1}={\begin{pmatrix}1\\0\\2\end{pmatrix}}\,\,{\text{  and }}\,\,v_{2}={\begin{pmatrix}0\\1\\3\end{pmatrix}}.

We have ${}\Vert {v_{1}}\Vert ={\sqrt {5}}$ ; therefore,

{}u_{1}={\frac {v_{1}}{\Vert {v_{1}}\Vert }}={\begin{pmatrix}{\frac {1}{\sqrt {5}}}\\0\\{\frac {2}{\sqrt {5}}}\end{pmatrix}}\,

is the corresponding normed vector. According to^[3] orthonormalization process, we set

{}{\begin{aligned}w_{2}&=v_{2}-\left\langle v_{2},u_{1}\right\rangle u_{1}\\&={\begin{pmatrix}0\\1\\3\end{pmatrix}}-\left\langle {\begin{pmatrix}0\\1\\3\end{pmatrix}},{\begin{pmatrix}{\frac {1}{\sqrt {5}}}\\0\\{\frac {2}{\sqrt {5}}}\end{pmatrix}}\right\rangle {\begin{pmatrix}{\frac {1}{\sqrt {5}}}\\0\\{\frac {2}{\sqrt {5}}}\end{pmatrix}}\\&={\begin{pmatrix}0\\1\\3\end{pmatrix}}-{\frac {6}{\sqrt {5}}}{\begin{pmatrix}{\frac {1}{\sqrt {5}}}\\0\\{\frac {2}{\sqrt {5}}}\end{pmatrix}}\\&={\begin{pmatrix}0\\1\\3\end{pmatrix}}-{\begin{pmatrix}{\frac {6}{5}}\\0\\{\frac {12}{5}}\end{pmatrix}}\\&={\begin{pmatrix}-{\frac {6}{5}}\\1\\{\frac {3}{5}}\end{pmatrix}}.\end{aligned}}

We have

{}\Vert {w_{2}}\Vert =\Vert {\begin{pmatrix}-{\frac {6}{5}}\\1\\{\frac {3}{5}}\end{pmatrix}}\Vert ={\sqrt {{\frac {36}{25}}+1+{\frac {9}{25}}}}={\sqrt {\frac {70}{25}}}={\frac {\sqrt {14}}{\sqrt {5}}}\,.

Therefore,

{}u_{2}={\frac {\sqrt {5}}{\sqrt {14}}}{\begin{pmatrix}-{\frac {6}{5}}\\1\\{\frac {3}{5}}\end{pmatrix}}={\begin{pmatrix}-{\frac {6}{\sqrt {70}}}\\{\frac {\sqrt {5}}{\sqrt {14}}}\\{\frac {3}{\sqrt {70}}}\end{pmatrix}}\,

is the second vector of the orthonormal basis.

Corollary

Let ${}V$ be a finite-dimensional ${}{\mathbb {K} }$ -vector space, endowed with an inner product. Then there exists an orthonormal basis

of

{}V

.

Proof

This follows directly from Theorem 32.9 .

\Box

Therefore, in a finite-dimensional vector space with an inner product, one can always extend a given orthonormal system to an orthonormal basis; see exercise *****.

Corollary

Let ${}V$ be a finite-dimensional ${}{\mathbb {K} }$ -vector space, endowed with an inner product, and let ${}U\subseteq V$ denote a linear subspace. Then, we have

{}V=U\oplus U^{\perp }\,,

that is, ${}V$ is the direct sum of ${}U$ and its

orthogonal complement.

Proof

From ${}u\in U\cap U^{\perp }$ we get directly

{}\left\langle u,u\right\rangle =0\,,

thus ${}u=0$ . This means that the sum direct. Let ${}u_{1},\ldots ,u_{k}$ be an orthonormal basis of ${}U$ . We extend it to an orthonormal basis ${}u_{1},\ldots ,u_{n}$ of ${}V$ . Then we have

{}U^{\perp }=\langle u_{k+1},\ldots ,u_{n}\rangle \,;

Therefore, ${}V$ is the sum of the linear subspaces.

\Box

For the following statement, compare also Lemma 15.6 and exercise *****.

Corollary

Let ${}V$ be a ${}{\mathbb {K} }$ -vector space, endowed with an inner product

{}\left\langle -,-\right\rangle

. Then the following statements hold.

For a linear subspace ${}U\subseteq U'\subseteq V$ , we have
${}U^{\perp }\supseteq U'^{\perp }\,.$
We have ${}0^{\perp }=V$ and ${}V^{\perp }=0$ .
Let ${}V$ be finite-dimensional. Then we have
${}{\left(U^{\perp }\right)}^{\perp }=U\,.$
Let ${}V$ be finite-dimensional. Then we have
${}\dim _{K}{\left(U^{\perp }\right)}=\dim _{K}{\left(V\right)}-\dim _{K}{\left(U\right)}\,.$

Proof

See Exercise 32.26 .

\Box

Orthogonal projections

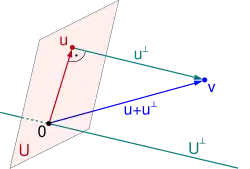
For a finite-dimensional ${}{\mathbb {K} }$ -vector space, endowed with an inner product, and a linear subspace ${}U\subseteq V$ , there exists an orthogonal complement ${}U^{\perp }$ , and the space has, according to Corollary 32.12 , the direct sum decomposition

{}V=U\oplus U^{\perp }\,.

The projection

p_{U}\colon V\longrightarrow U

along ${}U^{\perp }$ is called the orthogonal projection onto ${}U$ . This projection depends only on ${}U$ , because the orthogonal complement is uniquely determined. Often, the composed mapping ${}V\rightarrow U\rightarrow V$ is also called the orthogonal projection onto ${}U$ . An orthogonal projection is also described as dropping a perpendicular onto ${}U$ .

Lemma

Let ${}V$ be a finite-dimensional ${}{\mathbb {K} }$ -vector space, endowed with an inner product, and let ${}U\subseteq V$ denote a linear subspace with an orthonormal basis ${}u_{1},\ldots ,u_{m}$ of ${}U$ . Then the orthogonal projection onto ${}U$ is given by

{}p_{U}(v)=\sum _{i=1}^{m}\left\langle v,u_{i}\right\rangle u_{i}\,.

Proof

We extend the basis to an orthonormal basis ${}u_{1},\ldots ,u_{n}$ of ${}V$ . The orthogonal complement of ${}U$ is

{}U^{\perp }=\langle u_{m+1},\ldots ,u_{n}\rangle \,.

Due to Lemma 32.8 , we have

{}v=\sum _{i=1}^{n}\left\langle v,u_{i}\right\rangle u_{i}={\left(\sum _{i=1}^{m}\left\langle v,u_{i}\right\rangle u_{i}\right)}+{\left(\sum _{i=m+1}^{n}\left\langle v,u_{i}\right\rangle u_{i}\right)}\,.

Therefore, ${}\sum _{i=1}^{m}\left\langle v,u_{i}\right\rangle u_{i}$ is the projection onto ${}U$ along ${}U^{\perp }$ .

\Box

Footnotes

↑ For this, one has to accept that the length defined via the inner product coincides with the intuitively defined length, which rests on the elementary-geometric Theorem of Pythagoras.
↑ Here, ${}\langle -\rangle$ denotes the linear subspace spanned by the vectors, not the inner product.
↑ Often, it is computationally easier, first to orthogonalize and then to normalize at the very end; see example *****.

<< \| Linear algebra (Osnabrück 2024-2025)/Part II \| >> PDF-version of this lecture Exercise sheet for this lecture (PDF)

[1] For this, one has to accept that the length defined via the inner product coincides with the intuitively defined length, which rests on the elementary-geometric Theorem of Pythagoras.

[2] Here, ${}\langle -\rangle$ denotes the linear subspace spanned by the vectors, not the inner product.

[3] Often, it is computationally easier, first to orthogonalize and then to normalize at the very end; see example *****.

[1]

[2]

[3]