Inverse-producing extensions of Topological Algebras/Algebra of polynomials

Introduction

A polynomial algebra $A[t]$ is a vector space of polynomials, where the coefficients come from the given algebra $A$ . The polynomial algebra $A[t]$ is an essential tool to construct an algebra extension $B$ of $A$ in which a given $z\in A$ is invertible if it satisfies certain topological invertibility criteria.

Remark: Algebra expansion

In the construction of algebra extension in which a $z\in A$ is invertible, the first step is to consider the algebra of polynomials $A[t]$ . The following figure shows how the algebra extension $B$ is constructed over the polynomial algebra.

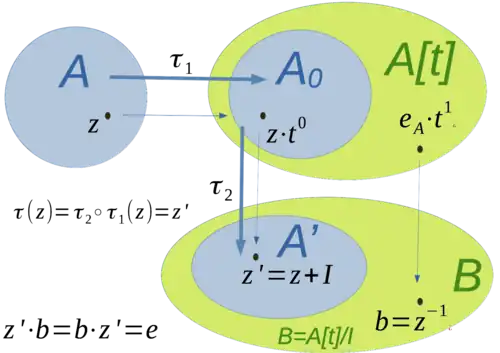
Algebra extension and polynomial algebras with coefficients in A

Algebraic closure

We only extend the algebra $A$ to contain an additional element $t\notin A$ , which is to be contained in an algebra extension $B$ of $A$ . Since multiplication and addition must be completed in $B$ , polynomials result from multiplications $a\cdot t$ and $t\cdot t=t^{2}$ with coefficients $a\in A$ n, which must be contained as summands $a_{n}\cdot t^{n}$ as polynomials in the algebra expansion.

Extension of the algebra

This implies the closure of the

multiplicative linkage of $t$ with itself and therefore $t^{n}$ with $n\in \mathbb {N}$ must also be in $B$ again,
the arbitrary multiplicative links of $t^{n}\in B$ with elements from $A$ lie again in $B$ , i.e. $a_{n}\cdot t^{n}\in B$ .
the additive algebraic algebraic closure also eventually requires that additive links from $a_{n}\cdot t^{n}\in B$ lie again in $B$ .

Polynomials with coefficients from the given algebra

Out of this necessity, one considers polynomials with coefficients from $A$ as the first step in constructing an algebra expansion in which a $z$ can be invertible.

Polynomial algebra

We now consider, for a given topological algebra ${\textstyle \left(A,\left\|\cdot \right\|_{\mathcal {A}}\right)\in {\mathcal {K}}(\mathbb {K} )}$ , the set of polynomials with coefficients in $A$ .

p(t)=\sum _{k=0}^{n}p_{k}\cdot t^{k}{\mbox{ with }}p_{k}\in A{\mbox{ for }}k\in \{0,1,...,n\}

and power series with coefficients in algebra $A$ .

p(t)=\sum _{k=0}^{\infty }p_{k}\cdot t^{k}{\mbox{ with }}p_{k}\in A{\mbox{ for }}k\in \mathbb {N} _{o}

Degree of polynomials

First of all, polynomials would be more formally notated in the above form with $n\in \mathbb {N} _{o}$ and with $p_{n}\not =0_{A}$ $n$ would indicate the degree of the polynomial. For the Cauchy product of two polynomials $p,q\in A[t]$ , however, this notation is unsuitable, since in the addition and multiplication two polynomials $p,q\in A[t]$ the handling of the degree entails additional formal overhead, which, however, does not matter for the further considerations of algebra expansions.

Notation for the polynomial algebra

Therefore, polynomials are defined as follows over "finite" sequences $c_{oo}(A)$ , which from an index bound $n\in \mathbb {N} _{o}$ consists only of the zero vector $0_{A}$ in $A$ .

p(t)=\sum _{k=0}^{\infty }p_{k}\cdot t^{k}{\mbox{ with }}(p_{k})_{k\in \mathbb {N} _{0}}\in c_{oo}(A)

Cauchy product

Given, in general, two polynomials $p,q$ with coefficients from ${\textstyle A}$ .

p(t):=\sum _{k=0}^{\infty }p_{k}\cdot t^{k}{\mbox{ und }}q(t):=\sum _{k=0}^{\infty }q_{k}\cdot t^{k}

Then Cauchy product of $p,q$ is defined as follows:

p(t)\cdot q(t):=\sum _{n=0}^{\infty }\left(\sum _{k=0}^{n}p_{k}\cdot q_{n-k}\right)t^{n}.

Page Information

You can display this page as Wiki2Reveal slides

Wiki2Reveal

The Wiki2Reveal slides were created for the Inverse-producing extensions of Topological Algebras' and the Link for the Wiki2Reveal Slides was created with the link generator.

This page is designed as a PanDocElectron-SLIDE document type.
Source: Wikiversity https://en.wikiversity.org/wiki/Inverse-producing%20extensions%20of%20Topological%20Algebras/Algebra%20of%20polynomials
see Wiki2Reveal for the functionality of Wiki2Reveal.