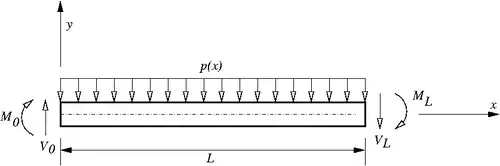
Solution:
Taking the first variation of the functional  , we have
, we have

Integrating the first terms of the above expression by parts, we have,

Integrating by parts again,

Expanding out,

Rearranging,
![{\displaystyle {\begin{aligned}\delta \Pi =&\int _{0}^{L}\left[(EI~y^{''})^{''}-p\right]\delta y~dx+\left[M_{0}-EI~y^{''}(0)\right]\delta y^{'}(0)+\left[EI~y^{''}(L)-M_{L}\right]\delta y^{'}(L)\\&+\left[(EI~y^{''})^{'}(0)-V_{0}\right]~\delta y(0)+\left[V_{L}-(EI~y^{''})^{'}(L)\right]~\delta y(L)\end{aligned}}}](../ade4c831fe06da023044af5b700ca286d759b192.svg)
Using the principle of minimum potential energy, for the functional  to have a minimum, we must have
to have a minimum, we must have  . Therefore, we have
. Therefore, we have
![{\displaystyle {\begin{aligned}0=&\int _{0}^{L}\left[(EI~y^{''})^{''}-p\right]\delta y~dx+\left[M_{0}-EI~y^{''}(0)\right]\delta y^{'}(0)+\left[EI~y^{''}(L)-M_{L}\right]\delta y^{'}(L)\\&+\left[(EI~y^{''})^{'}(0)-V_{0}\right]~\delta y(0)+\left[V_{L}-(EI~y^{''})^{'}(L)\right]~\delta y(L)\end{aligned}}}](../912a6e7b1dd8b8127a8dfcfc5ffa6e9a446d5247.svg)
Since  and
and  are arbitrary, the Euler equation
for this problem is
are arbitrary, the Euler equation
for this problem is

and the associated boundary conditions are

and